Wie lauten die Koordinaten des Bildpunktes P’

Question

Gegeben sind zwei Kreise k(M, r) mit M(-4; 4), r = 4 cm und k*(M*, r*) mit
M*(-2,5; 4), r* = 1,5 cm.

a) Wie lauten die Koordinaten des Bildpunktes P’, wenn P(-2; 4) am Kreis
k(M, r) gespiegelt wird? (K)

b) Konstruieren Sie zu drei selbst gewählten Punkten des Kreises k*(M*, r*) die Bildpunkte bei Inversion am Kreis k(M, r) und beschreiben Sie für das Finden eines Bildpunktes die Konstruktionsschritte. Welche Bildfigur k*’ entsteht, wenn k* an k gespiegelt wird?

Answer 1

Hallo Leonie,

Die Kreisspiegelung des Punktes \(P(-2;4)\) am Kreis \(k\) (rot) führt zum Punkt \(P'(4;4)\), wie man in diesem Bild sieht

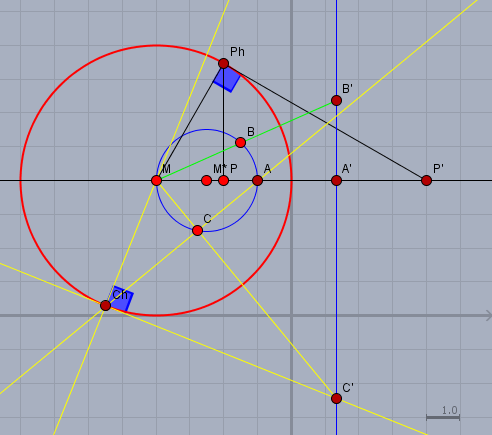
Dazu habe ich durch den Mittelpunkt \(M\) von \(k\) und \(P\) eine Gerade gezogen und auf ihr das Lot (schwarz) durch \(P\) errichtet. Das Lot schneidet \(k\) in \(P_h\). Zieht man nun durch \(P_h\) und \(M\) eine weiter Gerade und errichtet in \(P_h\) das Lot (schwarz) auf ihr, so schneidet das Lot in \(P_h\) die Gerade durch \(MP\) in \(P'\).

Auf \(k*\) (blau) habe ich drei Punkte \(A\), \(B\) und \(C\) gewählt. Deren Bilder an \(k\) sind \(A'\), \(B'\) und \(C'\). Für \(C\) habe ich die Konstruktion noch mal ausführlich dargestellt (die gelben Geraden). Die Bildpunkte liegen auf einer Geraden, was daran liegt, dass \(M\) auf \(k*\) liegt. das Bild eines Kreises, der den Mittelpunkt des Spiegelkreises enthält, ist eine Gerade. Das wird vielleicht klarer, wenn Du versucht den Punkt \(M\), oder einen Punkt auf \(k*\), der sehr dicht an \(M\) liegt zu spiegeln.

Gruß Werner