Folgende Aufgabe ist gegeben:
Bei einer Silvesterparty werden aufgrund eines akuten Budgetmangels nur 59% der Raketen von einem renommierten Markenhersteller bezogen, die restlichen sind billige No-Name-Raketen. 6% der Marken-Raketen und 14% der Billig-Raketen sind "Blindgänger", d.h. die Raketen können trotz Abbrennen der Zündschnur nicht abgefeuert werden.
Als die letzte Rakete angezündet wird, beginnt diese zwar, ganz fürchterlich nach Schwefel zu stinken, kann aber nicht abgefeuert werden. Mit welcher Wahrscheinlichkeit handelt es sich dabei um eine der Billig-Raketen?
(Bitte geben Sie das Ergebnis in Prozent an.)
Und hier mein Lösungsweg:
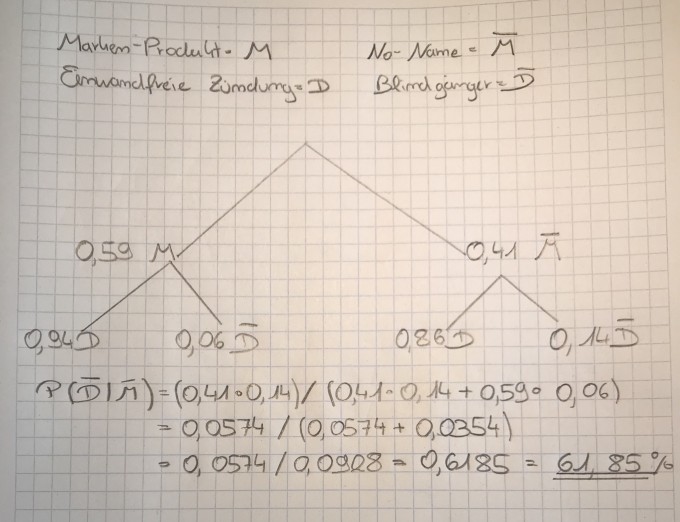
Kann das so stimmen?
MatheJoe