Basis von Untervektorraum berechnen

Question

Erstmal die Aufgabenstellung:

Es sei V = {f ∈ K[X] | deg(f) ≤ 3} der Vektorraum der Polynome über einem Körper K von Grad höchstens drei. Weiter seien
U₁ = <2x² - 2, 2x - 2x², -2x² + 4x -2>
U₂ = <-x³ + x² + 3x -1, -x³ + x² + x + 1>

Berechnen Sie eine Basis B₀ von U₁ ∩ U₂ und ergänzen Sie diese zu Basen B₁ und B₂ von U₁ bzw. U₂.

Ich weiß zwar wie ich allgemein vorgehen muss aber ich bin mir unsicher wie ich mit U₁ bzw. U₂  rechnen soll. Ich habe versucht sie in Vektorschreibweise zu bringen um damit die Basis berechnen zu können. Nun sind mir da 2 Möglichkeiten in den Sinn gekommen: Bei z.B. U₁ 

1) 

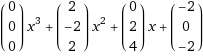
2) 

Einfach genau wie in U₂ nur, dass jeweils
-x³ + x²+ 3x -1 und -x³ + x² + x + 1
als Vektoren dargestellt werden.

Ist eine der Ideen die Richtige oder mache ich das komplett falsch?
Ich glaube zwar, dass Möglichkeit 2 richtig ist bin mir da aber sehr unsicher, ich würde mich über jegliche Hilfe sehr freuen.

Comments

Du puzzelst da alles wild durcheinander. Entweder Du rechnest mit Polynomen \(a_0+a_1x+a_2x^2+a_3x^3\) aus \(V\) oder mit Vektoren \((a_0,a_1,a_2,a_3)\) aus \(\mathbb{R}^4\). Im letzteren Falle kommen dann keine \(x\) mehr vor.

---

Ok, danke für die schnelle Antwort. Ich hätte sonst die ganze Aufgabe komplett falsch gemacht.

Answer 1

Schau mal dort:

https://www.mathelounge.de/511317/berechnen-eine-basis-erganzen-diese-basen-und-b2-von-u1-bzw

Und wenn du mit Spaltenvektoren rechnen willst, bedenke, dass 

die Polynome aus einem 4-dim-Raum sind.