Wie bestimme ich die Eckpunkte? (Vektorrechnung)

Question

 

ich habe eine Aufgabe bezüglich der Vektorrechnung - Drehungen im Raum.

Für den Würfel W gilt: 

W := [0, 1] × [0, 1] × [0, 1]  (--> wobei mir persönlich das leider überhaupt nichts aussagt?)

Nun soll man die Gerade betrachten, die durch den Nullpunkt und den Punkt g: =  (1, 1, 1) (als Spaltenvektor angegeben) geht. 

Der Würfel wird nun um 120 Grad um diese Achse (im Uhrzeigersinn von oben gesehen) gedreht. 

Wo sind dann die Eckpunkte des gedrehten Würfels? 

Es wäre echt super nett, wenn mir jemand weiterhelfen könnte :)

Vielen Dank im Voraus!

Answer 1

[0, 1] ist die Menge aller Zahlen zwischen 0 und 1 (inklusive).

Mittels × werden Paare gebildet. Zum Beispiel  besteht die Menge {1,3,5} × {2,4} aus den Paaren (1,2), (3,2), (5,2), (1,4), (3,4), (5,4).

Drehung um eine Urspunggerade kannst du ausfüheren, indem du en Ortsvektor de Punktes mit \(\begin{pmatrix} n_1^2 \left(1-\cos\alpha\right) + \cos\alpha & n_1 n_2 \left(1-\cos\alpha\right) - n_3 \sin\alpha & n_1 n_3 \left(1-\cos\alpha\right) + n_2 \sin\alpha \\ n_2 n_1 \left(1-\cos\alpha\right) + n_3 \sin\alpha & n_2^2\left(1-\cos\alpha\right) + \cos\alpha & n_2 n_3 \left(1-\cos\alpha\right) - n_1 \sin\alpha \\ n_3 n_1 \left(1-\cos\alpha\right) - n_2 \sin\alpha & n_3 n_2 \left(1-\cos\alpha\right) + n_1 \sin\alpha & n_3^2\left(1-\cos\alpha\right) + \cos\alpha \end{pmatrix}\) multiplizierst. Dabei ist α der Winkel und (n₁,n₂,n₃)^T ein normierter Richtungsvektor der Geraden.

Answer 2

Hallo Chanelle,

Jede Drehung lässt sich über eine Drehmatrix realisieren. Fangen wir mal mit einer ganz einfachen Drehung um die Z-Achse um den Winkel \(\varphi\) an. Die zugehörige Rotationsmatrix \(R_z(\varphi)\) wäre

$$R_z(\varphi) = \begin{pmatrix} \cos \varphi & -\sin \varphi & 0\\ \sin \varphi & \cos \varphi & 0\\ 0 & 0 & 1\end{pmatrix}$$ Das bedeutet, dass ein Punkt \(A=(1;0;0)^T\), der um \(\varphi\) gedreht wird, zu \(A'\) wird

$$A' = R_z \cdot A $$ In unserem Beispiel soll um 120° gedreht werden. \(R_z\) wird dann zu

$$R_z(120°) = \begin{pmatrix} -\frac12 & \frac12 -\sqrt{3} & 0\\ \frac12 \sqrt{3}& -\frac12 & 0\\ 0 & 0 & 1\end{pmatrix}$$ und ein \(A'(120°)\) wäre dann

$$A'(120°) = R_z(120°) \cdot A = \begin{pmatrix} -\frac12 \\ \frac12 \sqrt{3}\\ 0 \end{pmatrix}$$ Folgendes Bild zeigt den um z gedrehten Würfel mit den drei Punkten \(A\), \(B\) und \(F\). Der Punkt \(A'\) befindet sich an den berechneten Koordinaten.

 

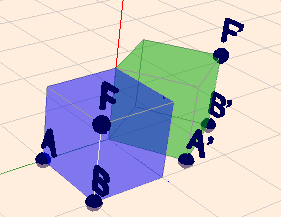
Jetzt soll aber um den Vektor durch \(F\) gedreht werden. Dazu bilde ich ein neues Koordinatensystem, dessen Z-Achse durch \(F\) geht und berechne die Koordinaten der Punkte in diesem System \(Q\). Anschließend wende ich die Drehung um Z an - genau wie oben - und transformiere das Ergebnis wieder zurück. Eine Drehmatrix D um 120° um den Vektor \((1;1;1)^T\) wäre dann allgemein:

$$D = Q \cdot R_z(120°) \cdot Q^{-1}$$ Die Z-Richtung von \(Q\) ist mit \((1;1;1)^T\) vorgegeben. Eine dazu senkrechte Richtung ist schnell gefunden: vertausche zwei Koordinaten und negiere eine davon - also z.B. \((1;-1;0)^T\) und den dritte (d.h. die Y-Richtung) Vektor bekommt man über das Kreuzprodukt der beiden:

$$Q \approx \begin{pmatrix} 1 & 1 & 1\\ -1 & 1 & 1\\ 0 & -2 & 1\end{pmatrix} $$ Die Richtungen der Basisvektoren sind nun korrekt, jetzt müssen sie noch normiert werden, damit sie als Orthogonal-Basis taugen $$Q = \begin{pmatrix} \frac12 \sqrt{2} & \frac16 \sqrt{6} & \frac13 \sqrt{3}\\ -\frac12 & \frac16 \sqrt{6} & \frac13 \sqrt{3}\\ 0 & -\frac13 \sqrt{6} & \frac13 \sqrt{3}\end{pmatrix} $$ Folgendes Bild zeigt die Basisvektoren (klick auf das Bild):

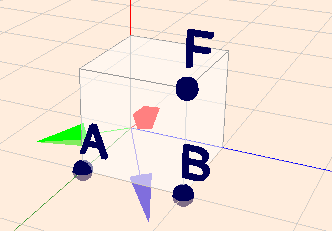
Man kann sehen, dass die Z-Achse von \(Q\) auf \(F\) zeigt und das alle Vektoren senkrecht auf einander stehen. Jetzt ist \(Q\) eine Orthogonal Matrix. Die hat den Vorteil , das ihre Inverse identisch mit der transponierten ist: \(Q^{-1} = Q^T\). Das setze ich in obige Gleichung ein und bekomme eine recht einfache Matrix \(D\)

$$D = Q \cdot R_z(120°) \cdot Q^{-1} = \begin{pmatrix} 0 & 0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0\end{pmatrix}$$

und wenn ich nun die drei Punkte \(A\), \(B\) und \(F\) (stellvertretend für alle anderen) mit \(D\) multipliziere bekommt man:

$$[A';B';F'] = D \cdot [A;B;F] = \begin{pmatrix} 0 & 0 & 1\\ 1 & 1 & 1\\ 0 & 1 & 1\end{pmatrix}$$ Gruß Werner