Folgendes Problem:
Zwei Personen gehen jeweils zu einer zufälligen Zeit zwischen 3 und 5 Uhr zum Arzt und haben jeweils eine Behandlungszeit von 30 Minuten. Wie groß ist nun die Wahrscheinlichkeit, dass einer der Patienten warten muss, wenn sonst keine Patienten zum Arzt gehen.
Der Ansatz läuft nun über ein den Flächeninhalt alle möglichen Ereignisse im Rechteck [3,5] x [3,5]. Setzen wir x:Erster Patient(Uhrzeit) y:Zweiter Patient(Uhrzeit) , dann ergeben sich als mögliche Gegenereignisse (x,y) mit |x-y| >1/2 und x,y im Intervall [3,5]
gezeichnet sieht das ganze dann so aus:
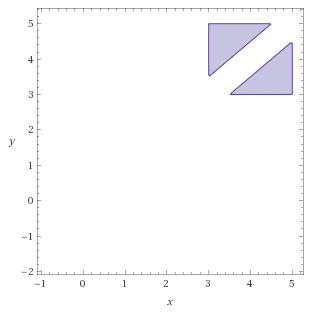
Die Wahrscheinlichkeit bestimmt sich nun aus: Fläche des Ereignisses / Gesamtfläche([3,5]x[3,5]) .
EDIT: Keine Fehler in der Rechnung. ( 1 - oben gezeichnete Fläche ) = Fläche des Ereignis.