Ableitung von R(R1,R2) = (R1*R2)/(R1 + R2)

Question

Schönen guten Abend :) 
Habe gestern bezüglich ableiten schon mal etwas gefragt, könntet ihr gegebenfalls hier nochmals helfen?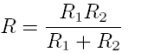  

Ich würde gerne nach R1, und R2 ableiten. Will es ungerne mit der Quotientenregel machen. 
Könnte man das ganze auch so schreiben ? 

R= R1*R2 * ( R1 + R2 ) ^-1  ?? Und damit weiter vorgehen ? Weiß bloß nicht wie ich weiter vor gehen soll. 

Wenn ich zum Beispiel nach R2 ableite. Bleibt doch R1 * R2 vorhanden und dann -1 * ( R1 + R2 ) ^-2 + 0 oder? 

Liebe Grüße   

Answer 1

Habe mal nach R1 abgeleitet:

(dabei wird R2 wie eine Konstante betrachtet)

Comments

Die drittletzte Zeile erhält man natürlich mit der Quotientenregel sofort.

@bUu2188

> Will es ungerne mit der Quotientenregel machen. 

Warum ?  :-) 

---

Habe es nun mit der Quotientenregel gelöst :D Ich habe nur Schwierigkeiten z.B Wenn Ich nach R1 ableite lautet die Quotientenregel ja : h(x) * g'(x) - g(x) * h'(x) / h(x)^2 

was ich bei g'(x) machen muss, wenn die Variablen als Multiplikation da stehen als wenn Sie zum Beispiel als Addition vorhanden sind. Dort muss ich sehr aufpassen. Ich merke mir es immer so ( hoffentlich richtig ) das bei Multiplikation sie als "Paar" zählen und bei Addition einzeln zu betrachten sind. bei g'(x) fällt das R1 weg und es bleibt nur R2 und bei Addtion h'(x) +1 .

Liebe Grüße 

---

die Quotientenregel ja : (h(x) * g'(x) - g(x) * h'(x)) / h(x)^2  . Punkt- vor Strichrechnung!

Tipp: Wenn du nach R1 ableitest, kannst du R2 durch z.B. 7 ersetzen und R1 durch x.

Bei der Ableitung nach R2 dann umgekehrt. 

Zum Schluss aber alles nochmals schön mit R1 und R2 abschreiben. 

Answer 2

Ich empfehle, um die Übersicht zu
behalten, bei Ableitungen nach der Produkt- oder
Quotientenregel die beteiligten Terme
vorher zu bestimmen und hinzuschreiben.

u = ..
u ´= ...
v = ...
v ´= ...

Hier meine Ableitung für R2

Comments

Falls es für dich einfacher ist nach x abzuleiten
dann ersetze R2 durch x und
schreibe die erste Formel als

R ( x ) = ( R1 * x ) / ( R1 + x )

Beim Ergebnis x wieder durch R2 ersetzen.

---

Gern geschehen.
Falls du weitere Fragen hast dann stelle
sie wieder ein.

Answer 3

Wegen

$$ R = \dfrac{R_1R_2}{R_1+R_2} = \dfrac{1}{\dfrac{1}{R_1}+\dfrac{1}{R_2}} $$lässt sich die Ableitung (hier nach R_1) mithilfe der Reziprokenregel in Verbindung mit der Kettenregel bilden und anschließend geeignet vereinfachen:

$$ \dfrac{\partial R}{\partial R_1} = \dfrac{\partial}{\partial R_1} \left(\dfrac{1}{\dfrac{1}{R_1}+\dfrac{1}{R_2}}\right) = \dfrac{-1}{\left(R_1\right)^2} \cdot \dfrac{-1}{\left(\dfrac{1}{R_1}+\dfrac{1}{R_2}\right)^2} = \dots = \left( \dfrac{R_2}{R_1+R_2} \right)^2 $$