Du schriebst: "Ich will wissen wie man auf diese Rechnung gekommen ist. Wir haben A und B gegeben und will wissen wie diese gleichung aufgestellt wurde, also auf dieses x=..."
Für die Parameterform benötigst Du einen Richtungsvektor \(\vec{r}\). Diesen kannst Du aus der Differenz zweier unterschiedlicher aber ansonsten beliebiger Punkte der Gerade bestimmen. So ist z.B.:
$$\vec{r} = \vec{B} - \vec{A} = \begin{pmatrix} 1\\ 3\\ 3\end{pmatrix} - \begin{pmatrix} 1\\ 2\\ 4\end{pmatrix} = \begin{pmatrix} 1-1\\ 3-2\\ 3-4\end{pmatrix}= \begin{pmatrix} 0\\ 1\\ -1\end{pmatrix}$$ Als 'Stützpunkt' kannst Du einen weiteren wieder beliebigen Punkt wählen, also auch \(A\). Damit erhält man eine (von vielen) Parameterform dieser Geraden
$$\vec{x} = \vec{A} + \lambda \cdot \vec{r} = \begin{pmatrix} 1\\ 2\\ 4\end{pmatrix} + \lambda \cdot \begin{pmatrix} 0\\ 1\\ -1\end{pmatrix}$$
"Ich will nur wissen wie man auf \((0|3|2)^T\) kommt." \((0|3|2)^T\) ist kein Richtungsvektor der Geraden - das ist falsch.
Anbei das Szenario nochmal in Geoknecht3D (klick auf das Bild und drehe die Szene mit der Maus)
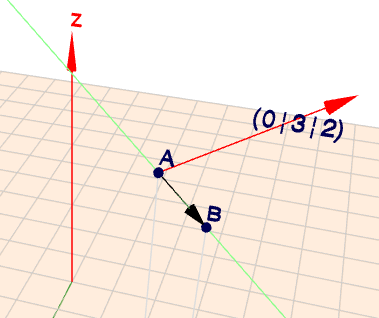
oben siehst Du die Gerade (grün), die durch die Punkte \(A\) und \(B\) verläuft. Als Richtungsvektor (schwarz) ist hier \(\vec{B}-\vec{A}\) gewählt. Der rote Vektor \((0|3|2)^T\) ist offensichtlich kein Richtungsvektor für diese Gerade.