Eine Fläche (Gitternetz) um einen zentralen Punkt krümmen. Gleitschirm und dessen Trimmung.

Question

Eine Fläche (Gitternetz) um einen zentralen Punkt krümmen. Gleitschirm und dessen Trimmung.

Ich schreibe ein kleines Programm zur grafischen Darstellung eines Gleitschirms und dessen "Trimmung".

Aus den Herstellerangaben (Fläche, Spannweite, Zellenanzahl, Streckung) kann ich die Form der ausgelegten Fläche recht genau errechnen.

Das Profil des Gleitschirms im Flug (Krümmung um die X und Y Achse) wird durch die Länge der Leinen bestimmt, die ausgehend von zwei Karabinern (Anknüpfpunkte rechts und links am Pilotengurt) zu den Loops (Anknüpfpunkte in der Schirmfläche) reichen.

Vereinfacht dargestellt:
Ich habe eine definierte Fläche mit Anknüpfpunkten, Außenmaße und X/Y Koordinaten der Anknüpfpunkte sind gegeben.
Die X/Y Koordinaten der Anknüpfpunkte am Pilotengurt(Karabiner ) sind ebenfalls bekannt.

Die Länge der Leinen die vom Karabiner zum jeweiligen Anknüpfpunkt reichen, sind Sollwerte des Herstellers. Die tatsächliche Länge soll gemessen, und so die Trimmung des Schirms grafisch dargestellt werden. Die ersten beiden zu berechnenden Punkte wären jene, welche am nächsten zur Z-Achse des Karabiners liegen. Die Länge der jeweils zugehörigen Leine wäre dann meine Hypotenuse und ich könnte mit einfacher Dreiecksberechnung den Abstand (Ankathete) des direkt über dem Karabiner liegenden Punktes berechnen. Dann müsste ich integral von einem Punkt zum nächsten rechnen, aber hier wird es dann schwierig:

Da die Positionen der Anknüpfpunkte in der Schirmfläche zueinander fix sind, würde eine verkürzte Leine auch die Lage bereits berechneter Punkte beeinflussen.

Hier fehlt mir sowohl Methodik als auch die Formeln wie ich die (X,Y,Z) Koordinaten der folgenden Anknüpfpunkte errechnen könnte.

1. ? Erst von Punkt zu Punkt in X-Richtung berechenen und dann die Lage in Y-Richtung? (Vektor von Karabiner zum letzten Punkt = Ankathete, Leinenlänge zum nächsten Punkt = Hypotenuse)

2. ? Alle Punkte zur senkrechten Z-Achse des Karabiners berechnen? (Z-Achse Karabiner = Ankathete, Leinenlänge = Hypotenuse)

3. ? Ist es komplizierter als gedacht und ich muss um jeden Punkt eine Kugel legen, auf deren Oberfläche irgendwo die Schnittpunkte von Leine und nächstem Punkt liegen?

4. ? Wie beeinflusst eine verkürzte Leine den vorher berechneten Punkt und muss ich zurück rechnen um diesen zu korrigieren?

Habe schon verschiedene Vorgehensweisen durchdacht ... die Erleuchtung will nicht kommen.

Zum besseren Verständnis habe ich das ganze mal mit dem Geoknecht vereinfacht dargestellt.

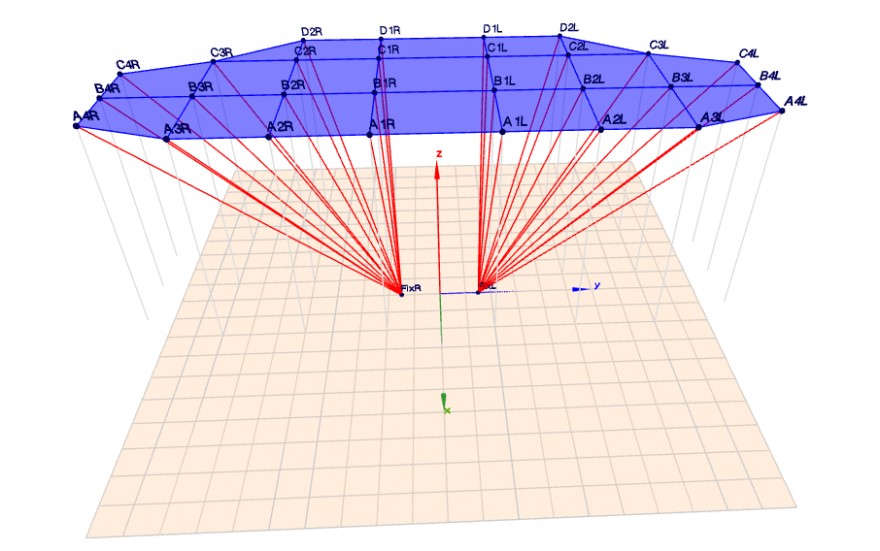
In meiner Darstellung ist die Fläche noch plan ausgelegt. Die Leinen(rote Linien)sind dementsprechend lang.

Für eine Beispielrechnung könnte man einfach die Leinen je Ebene nach hinten bzw. je Loop nach Außen um eine Einhet kürzen.

Hoffe mit dieser Aufgabe das Interesse und den Ergeiz des Ein oder Anderen geweckt zu haben.

Für Tipps, Rat, Hilfe und Schupser in die richtige Richtung wäre ich jedem Helfer sehr dankbar.

Gefragt 28 Feb 2018 von Isarwinkler

Hallo Kai,

Danke für's Lob.

Das geht sogar noch ein Stück cooler ;)

Hab mir gerade ein kleines Skript geschrieben, dass mir die Konturen meines Gleitschirms direkt in Geoknecht-Code ausspuckt.

Hier das Resultat:

Kommentiert 28 Feb 2018 von Isarwinkler

📘 Siehe "Koordinatensystem" im Wiki

2 Antworten

Ein anderes Problem?

Stell deine Frage

wächter · Answer 1 · 2018-02-28T18:42:56+0000

Hallo Wächter,

Danke für Dein Interesse.

Hab noch nie mit GeoGebra gearbeitet ... CAS, Konstruktionsvorlagen ... hört sich spannend an. Ich seh schon ich bin hier richtig :)

Ja, FixL und FixR sollen die Karabiner darstellen (Left/Right).

Ich erkläre mein Vorhaben gern noch etwas Detaillierter:

Das Programm das ich schreibe dient dazu, die Trimmung eines Gleitschirms zu prüfen.

Das Flugfähige Profil des Schirms entsteht zum einen durch den Innendruck, der beim Flug in den Zellen des Schirms entsteht und in der Hauptsache über die Belastung der Leinen durch das Gewicht des Piloten der quasi wie ein Pendel darunter hängt. Die Krümmung des Profils über die Quer und Längsachse sowie der Anstellwinkel gegen die Flugrichtung ist im wesentlichen abhängig von der genau abgestimmten Länge der Leinen.

Die Hersteller veröffentlichen Leinen-Protokolle, in denen das Sollmaß jeder Leine angegeben ist. Die Leinen eines Gleitschirms werden je nach Ebene unterschiedlich stark belastet. Besonders bei extremen Flugmanövern wie einer Steilspirale wirken bis zu 4G auf den Piloten und dementsprechend werden auch die Leinen gestreckt. Hinzu kommen Umwelteinflüsse wie UV-Strahlen, der Wechsel von Feuchtigkeit zu Trockenheit und starke Temperaturschwankungen (30º am Boden, 0º in 3000m Höhe) die enormen Einfluß auf die Länge der Leinen haben. Die Leinen der ersten beiden Ebenen (A und B) tragen die meiste Last und strecken sich mit der Zeit, die hinteren Ebenen (C, D und die Bremsleinen) werden hauptsächlich durch Temperaturunterschiede und dem Wechsel zwischen Feuchtigkeit und Trockenheit beansprucht und verkürzen sich zum Teil sogar. Das hat zur Folge, dass der Schirm sich im Laufe der Zeit "vertrimmt" und somit Profil und Anstellwinkel nicht mehr den vom Konstrukteur berechneten Werten entsprechen. Ein vertrimmter Schirm hat nicht mehr die optimale Gleitleistung (Gleitzahl = Wegstrecke bei 1m Höhenverlust, bei modernen Schirmen bis zu 12). Wichtiger ist jedoch der Sicherheitsaspekt: Durch ziehen der Bremsleinen steuert man den Schirm, bremst die Vorwärtsfahrt oder fängt Nickbewegungen ab. Mit zunehmendem Bremsweg nimmt auch die Kraft zu, gegen die man die Bremsleine nach unten zieht und jeder Pilot hat mit der Zeit ein Gefühl dafür (Muscel memory effect) bis wohin er die Bremse ziehen kann bis der Stallpunkt erreicht ist und die Strömung am Schirm abreißt. Ist der Schirm extrem vertrimmt und der Anstellwinkel ungünstig verändert, kann das zur Folge haben, dass der Stallpunkt wesentlich früher und bei geringerem Kraftaufwand als gewohnt erreicht wird.

Um die Trimmuni zu überprüfen nutzt man seit Jahren Handelsübliche Lasermessgeräte aus dem Baumarkt, die den Messwert sogar automatisch per Bluetooth in eine Exceltabelle auf dem Rechner schreiben. Hierzu wird der Tragegurt (Karabiner) an der Wand eingehängt, das Messgerät am entsprechenden Loop (Verknüpfungspunkt am Schirm) angehalten, der Laser auf die Messfläche am Tragegurt ausgerichtet und die Messung mit Knopfdruck ausgelöst. Die Messwerte werden dann unter Berücksichtigung einer Toleranz mit den Herstellerangaben verglichen und die Leinenlänge gegebenen Falls durch Ent- bzw. Einschlaufen am Leinenschloss korrigiert. Das funktioniert alles recht gut und wird seit Jahren so praktiziert. Das Trimmen eines Schirms braucht jedoch Erfahrung, Gefühl und eine gute Portion Vorstellungskraft da man ja nur Zahlen auf einem Excelsheet sieht. Nach jeder Trimmung werden die Leinen wieder vermessen. Man kommt schon mal durcheinander und es schleichen sich auch mal Denkfehler ein. Deshalb der Gedanke, die Trimmung des Schirms in einer 3D Grafik sichtbar zu machen. Mein Gedanke ist, ein Model mit den Soll-Werten darzustellen und eines mit den gemessenen Werten darüber zu legen, Fehler eventuell mit einem Faktor zu belegen um diese deutlicher sichtbar zu machen. Wettkampfpiloten trimmen ihren Schirm auch gern mal unabhängig der Herstellerangaben etwas schneller und eine grafische Darstellung in 3D macht dann recht deutlich sichtbar wo und wie weit man den Trimm verändert hat.

Kommentiert 28 Feb 2018 von Isarwinkler

Prinzipiell ja, ... die ideal Werte wären gegeben.

Woran ich grüble ist eben die Methodik und die entsprechenden Formeln um vom flach ausgelegten Schirm mit X/Y Koordinaten aller Punkte ins 3Dimensionale mit X/Y/Z Koordinaten für jeden Loop am Schirm.

Ich hatte auch den Gedanken, dass die Leinen des Ideal-Models quasi den Vektor geben und die tatsächliche Länge der Leine dann irgendwo auf der Strecke dieses Vektors liegen sollte. Die Vertrimmung wird in der Regel wohl auch nicht so dramatisch sein, dass sich der Winkel großartig ändern würde oder die Lage der umliegenden Punkte durch eine verkürzte Leine dramatisch beeinflusst würden. Realistisch wäre es jedoch, diesen Faktor ebenfalls zu berücksichtigen. Mit anderen Worten: verkürzt sich eine Leine dann würde das auch die Lage der benachbarten Punkte beeinflussen ... oder begehe ich da einen Denkfehler?

Siehe Link: https://www.matheretter.de/rechner/geozeichner?draw=punkt(1%7C3%20%22P1%22)%0Apunkt(4%7C4%20%22P2%22)%0Apunkt(7%7C4%20%22P3%22)%0Apunkt(10%7C3%20%22P4%22)%0Astrecke(1%7C3%204%7C4)%7BF00%7D%0Astrecke(4%7C4%207%7C4)%7BF00%7D%0Astrecke(7%7C4%2010%7C3)%7BF00%7D%0Astrecke(5.5%7C-8%201%7C3)%7B00F%7D%0Astrecke(5.5%7C-8%204%7C4)%7B00F%7D%0Astrecke(5.5%7C-8%207%7C4)%7B00F%7D%0Astrecke(5.5%7C-8%2010%7C3)%7B00F%7D%0Astrecke(1%7C3%201%7C7)%7B000%7D%0Astrecke(10%7C3%2010%7C7)%7B000%7D%0Astrecke(1%7C6%2010%7C6)%7B000%7D%0Atext(5.5%7C7%20%229%22)%0Apunkt(-2%7C3%20%22P4%22)%0Apunkt(-4%7C5%20%22P3%22)%0Apunkt(-7%7C5%20%22P2%22)%0Apunkt(-9%7C3%20%22P1%22)%0Astrecke(-2%7C3%20-4%7C5)%7BF00%7D%0Astrecke(-4%7C5%20-7%7C5)%7BF00%7D%0Astrecke(-7%7C5%20-9%7C3)%7BF00%7D%0Astrecke(-5.5%7C-8%20-2%7C3)%7B00F%7D%0Astrecke(-5.5%7C-8%20-4%7C5)%7B00F%7D%0Astrecke(-5.5%7C-8%20-7%7C5)%7B00F%7D%0Astrecke(-5.5%7C-8%20-9%7C3)%7B00F%7D%0Astrecke(-2%7C3%20-2%7C7)%7B000%7D%0Astrecke(-9%7C3%20-9%7C7)%7B000%7D%0Astrecke(-2%7C6%20-9%7C6)%7B000%7D%0Atext(-5.5%7C7%20%227%22)&scale=10

Kommentiert 28 Feb 2018 von Isarwinkler

Werner-Salomon · Answer 2 · 2018-03-02T11:37:57+0000

Hallo Isarwinkler,

mein Vorschlag zur Realisierung Deines Programms sieht wie folgt aus: Mache das ganze dynamisch.

Verpasse jedem Anknüpfpunkt einer Leine am Schirm eine hypothetische Masse $m_i$. Jede Masse hat eine Positionen $p_i$ und eine Geschwindigkeit $v_i$. Nun führe für jede Masse eine Kraft ein, die sie vom Karabiner weg nach oben zieht. Dann rechnest Du für jeden Punkt die Entfernung zu den Nachbarn und zum Karabiner aus und errechnest daraus Federkräfte, die Du alle inklusive der ersten Kraft addierst und daraus die Beschleunigung für jeden Punkt berechnest. Also formal, da $F= m \cdot a$, für jede Masse $i$:

$$\vec{a_i} = \frac{1}{m_i}\sum_k \vec{F}_{ik}$$ Zusätzlich führe noch eine Dämpfung $D$ ein, die gegen die Geschwindigkeit wirkt. D.h. für einen Index $k$ der Kräfte $\vec{F}_{ik} = -D \cdot \vec{v}_i$. Damit wird das System stabil!

Du startest mit der Geschwindigkeit 0 und einer angenommen Position - etwa so wie schon gezeichnet - und lässt es dann 'fliegen'. D.h. Du wählst ein Zeitintervall $\Delta t$ und rechnest aus, wie groß die Geschwindigkeit und die Position nach diesem Zeitintervall ist - heißt für alle $i$:

$$p_i := p_i + v_i \cdot \Delta t $$ $$v_i := v_i + a_i \cdot \Delta t$$ und das wird immer wiederholt. Dieser Algorithmus wäre das einfache Eulerverfahren. Wenn Du die Möglichkeit hast, kannst Du auch einen nummerischen Integrator nutzen. In C++ z.B. kann ich Dir ODEINT empfehlen.

Auf Grund der Dämpfung kommt das System zur Ruhe und nimmt dann den Zustand niedrigster Energie ein - oder anders ausgedrückt: Der Schirm steht! Nummerisch kannst Du das das prüfen, indem Du die Summe der kinetischen Energien betrachtest. Da die Massen alle konstant bleiben, reicht es aus, die Quadratesumme der Geschwindigkeiten zu bestimmen. Fällt sie unter einen voreingestellten Wert, bist Du fertig und kannst die Positionen übernehmen.

Der Nachteil des Verfahrens ist, dass es sich um eine nummerische Lösung handelt, die auch nicht 'exakt' sein wird. Da Du es aber für eine Darstellung in einer GUI benötigst, sollte das gar keine Rolle spielen. Du wirst auch noch etwas mit den Größen Masse und Dämpfung und $\Delta t$ herum spielen müssen, bis es 'rund' läuft. Für das $\Delta t$ solltest Du einen Wert wählen, der kleiner ist als ca. $\frac14 \sqrt{\frac{m_i}{K}}$; wenn $K$ die größte Federkonstante in Deinem System ist.

Der Vorteil ist, dass es programmatisch relativ leicht zu realisieren ist. Weiter wäre es denkbar das ganze auch dynamisch darzustellen. Wenn Du es schaffst die 'Kräfte schräg nach oben' einigermaßen realistisch durch die aerodynamischen Kräfte zu ersetzen, dürfte das ganze auch im Verhalten ziemlich realistisch aussehen! Z.B. bei Einfall einer Bö oder beim Ziehen an einer der Steuerleinen.

Noch eine Bemerkung zum Federmodell. Die Leinen werden natürlich nie auf Druck belastet. D.h. wenn die Entfernung einer der Aufhängepunkte zu seinem Karabiner unter die Leinenlänge fällt , dann ist die Leinenkraft =0. Bei den Verbindungen innerhalb des Schirms, wirst Du aber eine negative Kraft einführen müssen. Sonst wird der Schirm schlecht 'stehen'. Es ist ja auch in der Realität so, dass der Schirm aufgeblasen wird, und er sich damit Kräften, die ihn zusammendrücken, widersetzt.

Ich habe i.A. leider sehr wenig Zeit, sonst hätte mich selbst schon dran gemacht ;-). Und werde mich voraussichtlich erst in der nächsten Woche noch mal melden.

Immer eine glückliche Landung wünscht Dir

Werner

Eine Fläche (Gitternetz) um einen zentralen Punkt krümmen. Gleitschirm und dessen Trimmung.

2 Antworten

Ähnliche Fragen

Eingabetools:

Beliebte Fragen:

Heiße Lounge-Fragen: