Lineare Optimierung
Aufgabe
Schokolade wird hergestellt aus Kakao, Milchpulver und Zucker nach der Rezeptur:
| Vollmilch (x)
| Zartbitter (y)
|
| Kakao | 30%
| 60%
|
| Milchpulver | 20%
|
|
| Zucker | 50%
| 40%
|
Der Rohstoffbestand einer Confiserie beträgt 120kg Kakao, 30 kg Milchpulver und 90 kg Zucker. Das Vollmilch-Produkt erzielt einen Gewinn von 11,-€ pro kg, das Zartbitter Produkt einen Gewinn von 9,-€ pro kg. Wie viel kg Vollmilch bzw. Zartbitter sollen produziert werden, damit der Gewinn maximal ist. Wie hoch ist das Gewinnbetrag im Optimum?
Abfolge
1. Programm-Modell
Stellen sie die Gewinnfunktion Z auf und beschreiben sie den Zutatenverbrauch durch Ungleichungen.
2. Graphische Lösung [GeoGebra]
Bestimmen sie graphisch das Maximum und die herzustellenden Mengen.
3. Simplex-Algorithmus
Berechnen sie das Maximum mit dem Simplex-Algorithmus und bestimmen sie die
herzustellenden Mengen und die freien Kapazitäten.
1. Programm-Modell
Zielfunktion: Z(x, y) = 11 x +9 y; Z -> Max
Nebenbedingungen:
Kakao in kg: 30% x + 60% y <= 120
Milchpulver in kg: 20% x <= 30
Zucker in kg: 50% x + 40% y <= 90
Die Nebenbedingungen für Max-Programme müssen auf fi(X) <= bi gebracht werden - ggf.
(-1) fi(X) >= (-1) bi Ungleichzeichen umdrehen duch Multiplikation (-1)!
2. Graphische Lösung [GeoGebra]
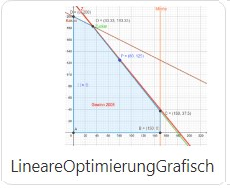GGB-Worksheet ↥
3. Simplex-Algorithmus
Start-Tableau (youtu.be/DYHUg0Zxe9A)
erstellen durch Einführung von Schupfvariablen si. Aus den Ungleichungen entstehen Gleichungen. Diese Gleichungen bilden das Start-Tableau.
| Kakao in kg: | 30% x +60% y + s1 = 120 |
| Milchpulver in kg: | 20% x + s2 = 30 |
| Zucker in kg: | 50% x + 40% y + s3 = 90 |
| Gewinn max | -Z(x, y) = -11 x - 9 y |
Simplex-Tableau lesen
Die Schlupfvariablen si stehen für die Restkapazität des Rohstoffes, der nach Produktion von x kg Vollmilch- und y kg Zartbitter noch zur Verfügung steht. Positive Schlupfvariablen definieren eine Basis für gültige Lösungen des Programms. Ein Produktionsprogramm von x=90, y=160 ergibt * X=(90,160,-3,12,-19) und zeigt eine unglültige Lösung an:
s1=-3 und s3=-19 (Kakao, Zucker fehlen)
Verbrauch und Rest
Milchpulver aufbrauchen: s2=0 >> x=30/20%=150. Der Vektor X=(150,0,75,0,15) ist EINE gültige Lösung unseres Gleichungsysytems im Tableau. Wir betrachten einen Eckpunkt des Lösungsgebietes - wie stellt sich diese Situation im Simplex-Tableau dar?
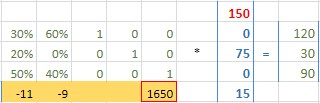
Darstellung im Tableau
Teile Zeile Milchpulver1/20% und übertrage x (mit Gauss-Schritt 0 in erster Spalte)
nach K,Z,G. In Zeile K Spalte b haben wir die Restmenge Kakao (75) und in Zeile Z die noch vorhandene Menge Zucker (15). Der Gewinn liegt bei 1650.
Das ist ein Schritt in Richtung Optimum noch 2 Rohstoffreste übrig. Die Bedeutung der Pivotzeile hat sich geändert - sie gibt jetzt nicht den Bestand an, sondern die Produktmenge. Mathematisch ausgedrückt: x wurde in die Basis aufgenommen, gegen s2 getauscht!
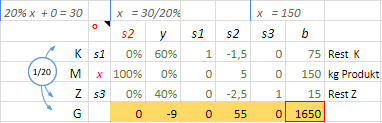
Machen wir daraus eine StrategieDie x-Spalte zu nehmen ist kein schlechter Plan, weil wegen dem größten Faktor in Z auch die größte Auswirkung in Richtung Gewinnmaximierung zu erwarten ist.
Die Pivotspalte wird durch den kleinsten Wert in der G-Zeile des Tableaus (G = -Z(x,y)) bestimmt.
Der b-Wert der Pivotzeile wird durch den Wert der Pivotsalte dividiert und von allen anderen subtrahiert - damit wir da nicht ins Minus kommen wäre es angebracht den kleinsten
positiven Quotienten zu nehmen (180). Die Pivotzeile wird durch den Wert der Pivotspalte dividiert damit in der Pivotzeile x Pivotpalte eine 1 steht und von den anderen Zeilen subtrahiert um die Pivotspalte zu 0 en.
Grundlagen Simplex-Algorithmus ↥
Google Sheet Javascript-Function und Excel VBA-Function
Simplex-Algorithmus Single Step für Google Sheets
@CustomFunction
=Simplex( Tableau )
Finde Pivotzeile,Pivotspalte im Simplex-Tableau
@CustomFunction
=SimplexFindPivot( Tableau )
Simplex-Tableau mit pivotZeile pivotSpalte berechnen
@param {Tableau} Simplex Tableau - Matrix Zeilen:Spalten.
@return Simplex Tableau berechnet mit pivotZeile, pivotSpalte.
@CustomFunction
=SimplexBerechneTableau( Tableau, pivotZeile, pivotSpalte )
