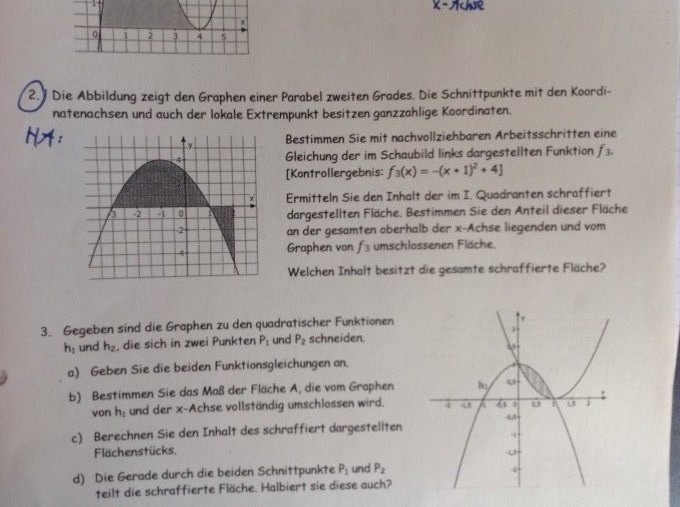
gegeben ist die Funktion: f3(x)= -(x+1)^2+4
Ermittelt werden soll die Fläche im ersten Quadranten. Dort hatte ich 1,667 FE.
Beim Anteil dieser Fläche hatte ich etwa 15%.
Wie berechne ich jetz die schraffierte Fläche, die außerhalb der Parabel und unterhalb der x-Achse liegt? (BILD sowie mein Lösungsansatz sind angefügt)
:)