f ( x ) = 1 / cos(x)^2
g ( x ) = 1
Prinzipiell mußt du nur die Differenzfunktion zwischen
f und g bilden und diese Integrieren.
Schnittpunkte = Intervallgrenzen
Der Graph
blau = f
rot = g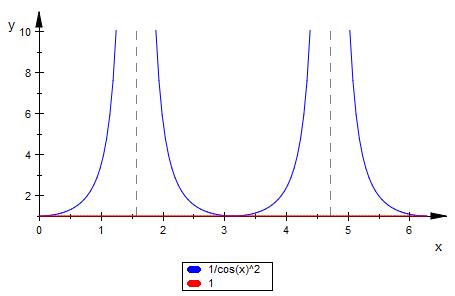
Zwischen PI/2 und PI ist ein uneigentliches
Integral vorhanden.

Der Flächeninhalt dürfte ∞ sein.
Prüfe ich aber nochmals nach.