Mathe-Rätsel #002: Happy Pi-Day!

Question

Heute ist Pi-Day (3/14). Und was könnte besser zu einem mathematischen Feiertag passen als ein kleines Rätsel?

Für ein \(\pi\)doku-Rätsel gelten folgende Regeln:

1.) Es dürfen nur die Ziffern \(1\) bis \(9\) und die Zahl \(\pi\) verwendet werden.

2.) In jeder Zeile dürfen die Ziffern von \(1\) bis \(9\) nur einmal vorkommen. \(\pi\) kommt in jeder Zeile genau dreimal vor.

3.) In jeder Spalte dürfen die Ziffern von \(1\) bis \(9\) nur einmal vorkommen. \(\pi\) kommt in jeder Spalte genau dreimal vor.

4.) In jedem schwarz umrandeten Block dürfen die Ziffern von \(1\) bis \(9\) nur einmal und \(\pi\) genau dreimal vorkommen.

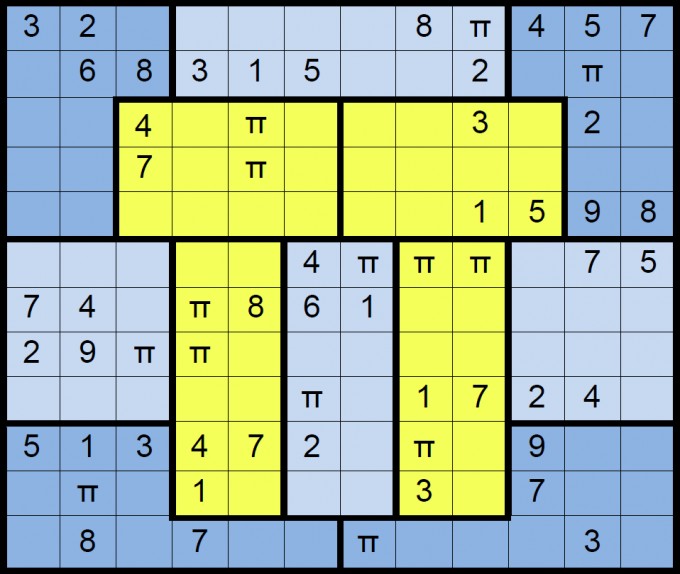
Viel Erfolg beim Rätseln!

Das Rätsel gibt es auch als PDF zum Ausdrucken (pidoku.pdf (0,2 MB) ).

Comments

Zusätzliche Challenge: Finde für jedes von Dir eingetragene \(\pi\) eine "kreative Darstellung" für \(\pi\). Z. B.: 

\(\pi = 4\cdot ((0.5)!)^2\)

---

Das ist eine zauberhafte Idee.

I ♥ π-DOKUS

---

> I ♥ π-DOKUS

Das freut mich :-) Die Kollegen von Stackexchange übrigens auch: https://puzzling.stackexchange.com/questions/61929/happy-pi-day-try-to-solve-this-pidoku ;-)

---

Hallo André,

Kann man π wirklich so darstellen?$$\pi = 4\cdot ((0.5)!)^2$$ Also ist es wirklich genau Pi?

---

Kann man π wirklich so darstellen?

https://www.wolframalpha.com/input/?i=(4*(0.5)!%5E2)+%3D%3D+pi :-)

---

Genauer wäre wohl

$$ \pi = 4 \cdot \Gamma(0.5)^2 $$

Auf jeden Fall ein sehr schönes Rätsel. Gefällt mir :)

---

Krass, das wusste ich gar nicht...

---

Genauer wäre wohl \(\pi=4\cdot \Gamma(0.5)^2\)

Das stimmt natürlich ;-) Der folgende Effekt ist bei \((0.5)!\) natürlich um Welten größer ;-)

https://www.youtube.com/watch?v=9CS7j5I6aOc

Was?!? Fakultäten gibt es auch bei Kommazahlen? Krass!

:-)

Auf jeden Fall ein sehr schönes Rätsel. Gefällt mir :)

Danke :-) Es freut mich, dass es Dir gefällt ;-)

---

Das mit den Gammafunktionen kenne ich schon. Wie man aus 0.5! machen kann..

Trotzdem bin ich Mindblown o.O

Ich dachte, dass nichts Pi darstellen kann

---

Trotzdem bin ich Mindblown o.O

Ziel erreicht :-)

\(\pi=-i\cdot\ln(-1)\)

---

Das find ich nicht besonders, wegen der imaginären Zahl....

Aber 4*((0.5)!)^2 find ich sehr interessant. Ich frag mich inwiefern das erklärbar ist.

---

Ich frag mich inwiefern das erklärbar ist.

https://www.youtube.com/watch?v=QhDDpSju3uY

Und ein wenig Magie von meiner Seite ...

---

Eine der schönsten Formeln der Mathematik

e^{i·π} = -1

Einfach mal nach π auflösen...

i·π = ln(-1)

-1·π = i·ln(-1)

π = - i·ln(-1)

---

Ja,

Euler's Identity, das kenne ich natürlich auch. Hierbei fehlt mir doch jegliches Wissen über komplexe Zahlen (i)

---

Hierbei fehlt mir doch jegliches Wissen über komplexe Zahlen (i)

Das klingt nach einem Mathe-Artikel ;-)

\(i\) ist zwar auch eine komplexe Zahl mit \(a=0\) und \(b=1\) (sofern die komplexen Zahlen in der Form \(z:=\underbrace{a}_{\Re}+\underbrace{b}_{\Im}\cdot i\) mit \(a,b\in\mathbb{R}\) dargestellt werden), doch zeitgleich ebenfalls die imaginäre Einheit \(i=\sqrt{-1}\). Diese taucht in der E-Technik häufig als \(j\) auf.

---

Haha, wenn das schon so anfängt.

Kann man das überhaupt ohne Vorwissen verstehen? Ich bin gerade einmal in der 10. Klasse. Ich habe noch einen langen Weg in der Mathematik vor Mir.

Aber ich bin immer offen für einen hohen Anspruch, denn dadurch lernt man am besten und effektivsten.

---

Kann man das überhaupt ohne Vorwissen verstehen?

Was genau?

Ich bin gerade einmal in der 10. Klasse.

Das war mir nicht bekannt. Ich hatte die komplexen Zahlen in der 11. Klasse kennengelernt ;-)

Ich habe noch einen langen Weg in der Mathematik vor Mir.

Ja. Zumal Du in der Schule ohnehin der Mathematik noch nicht begegnest. Dort lernt man nämlich nur "Rechnen" ;-)

Aber ich bin immer offen für einen hohen Anspruch

Wie ich in meinem Tutor-Seminar gelernt habe: Erst durch das Verlassen der Komfort-Zone (grün) und das Betreten der Lern-Zone (gelb) können wir neue Dinge erlernen und unsere Komfort-Zone erweitern :-)

---

Hmm, ich expandiere meine Komfortzonen je nach Interesse. Wenn mich etwas interessiert kämpfe ich mich durch, um es zu verstehen.

Zum Beispiel war ich ziemlich interessiert an Funktionsgleichungen, da ich diese in der Schule kennengelernt habe in Form von Quadratischen Funktionen. Irgendwann hab ich mir gedacht, was passiert eigentlich wenn ich dies und jenes mache. Ich hab schon so viel gelernt dadurch.

Learning by doing, kann man auf der Seite auch ganz gut anwenden, ohne dem Fragesteller dadurch irgendwie zu schaden.

EDIT:
Das ist gerade etwas off-topic

---

@Anton und André: Wenn ihr bei Wolframalpha Kommazahlen vermeidet, rechnet Wolframalpha genauer.

Hier Eingabe: https://www.wolframalpha.com/input/?i=(4*(1%2F2)!%5E2)

gibt unter anderem:

---

Es ist mal wieder so weit: Happy Pi-Day! :)

---

Ich finde es auch super, da es genau an Einsteins Geburtstag ist.