diese Aufgabe ist etwas schwieriger als die letzte.
1) erstelle eine aussagekräftig Skizze.
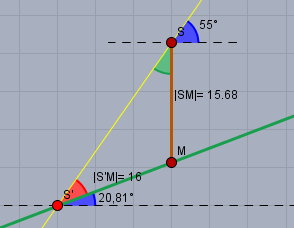
das war schon mal der schwerste Teil (nehme ich an). Der Mast (braun) steht im Punkt \(M\) am Hang (grün) und der Schatten seiner Spitze wird durch den Strahl (gelb) bei \(S'\) auf dem Hang projiziert.
2) beschreibe wie man die Höhe des Handymasts ermittelt
\(M\), \(S\) und \(S'\) bilden ein Dreieck von dem die Winkel und eine Seite (\(|S'M|=16\text{m}\)) bekannt sind. Gesucht ist eine weitere Seite \(|SM|\) des Dreiecks. D.h. hier bietet sich der Sinussatz an.
3) Berechnet die Höhe
$$\frac{|SM|}{\sin ( \colorbox{#FF3333}{55° - 20,81°})} = \frac{|S'M|}{\sin( \colorbox{#00DD00}{90°-55°})}$$ $$\Rightarrow |SM| = \frac{16 \text{m}}{\sin( \colorbox{#00DD00}{35°})} \sin( \colorbox{#FF3333}{34,19°}) \approx 15,68 \text{m}$$ Gruß Werner