Hallo Nama,
Du kannst diesen Winkel zechnerisch konstruieren. Der Trick besteht darin, alles auf ganze Zahlen zurück zu führen, die Du leicht auf dem Kästchengitter Deines Heftes oder mit einem Lineal erzeugen kannst.
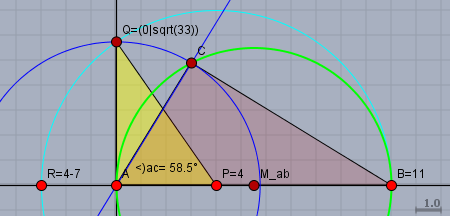
Das Ziel ist es, ein rechtwinkliges Dreieck zu zeichnen, desse Hypotenuse die Länge \(11\) und eine Kathete die Länge \(\sqrt{33}\) hat. Das rötliche Dreieck \(\triangle ABC\) erfüllt dies. Die Länge \(|AB|=11\) dürfte kein Problem sein. Die Länge \(|AC|=\sqrt{33}\) wird aus dem Dreieck \(\triangle APQ\) konstruiert. \(|AP|=4\) und \(|PQ|=7\). Daher ist
$$|AQ| = |AC| = \sqrt{ |PQ|^2 - |AP|^2} = \sqrt{ 7^2 - 4^2 } = \sqrt{33}$$
Alle roten Punkte liegen auf Gitterpunkten. \(Q\) ist der Schnittpunkt der zu \(AB\) Senkrechten durch \(A\) mit dem hellblauen Kreis um \(P\) mit dem Radius \(|RP|=7\). Und \(C\) ist der Schnittpunkt des blauen Kreises um \(A\) mit dem Radius \(|AQ|=\sqrt{33}\) mit dem Thaleskreis (grün) über \(AB\).
Der gesuchte Winkel ist dann \(\angle BAC\) bei Punkt \(A\), den kannst DU mit dem Geodreieck oder einem Winkelmesser ablesen.