Ein Grundstück liegt unterhalb des Straßenniveaus. Bestimmen Sie eine Funktion 3. Grades zur Gestaltung der Auffahrt, so dass am Übergang von dem Grundstück zur Auffahrt und am Übergang von der Auffahrt zum Straßenniveau kein Knick vorliegt.
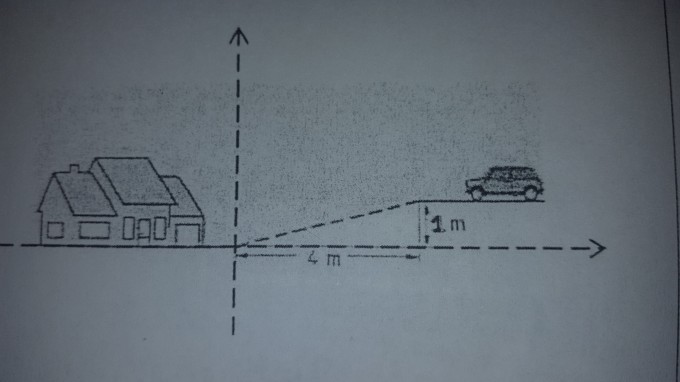
Aus dieser Aufgabe, kann ich jetzt die Punkte:
P1(0/0); P2(4/1) ablesen.
Da die Auffahrt keinen Knick haben soll, kann ich die Steigung auf 0 setzen.
f '(0)=0; f '(4)=0
Das ist, was ich bis jetzt gemacht habe und nicht mehr weiterkomme:
f(x) = ax^3+bx^2+xc+d
1) f(0) = d = 0
2) f(4) = 64a+16b+4c = 1
f '(x) = 3ax^2+2bx+c
3) f '(0) = c = 0
4) f '(4) = 48a+8b = 0 | *2
f '(4) = 96a+16b = 0
Und ab hier komme ich nicht mehr weiter. Ich weiß jetzt nicht, ob ich die c = 0 von 3) in 2) einsetzen kann, und wenn ich die Funktionen subtrahiere:
5) = 4) - 2)
32a+4c = -1 | +1 | - (4c)
32a + 1 = -4c | /(-4)
-8a -0,25 = c
dann weiß ich nicht mehr, ob ich dieses c jetzt in f(x) einsetzen kann und was danach gemacht werden soll, oder ob ich jetzt einen ganz falschen Ansatz habe.