zur Nullstelle:
Du schreibst leider nicht, welche Klassenstufe oder welchen Wissensstand der Mathematik vorliegt!?
a) Normale Schulklassen behandeln nur leichte Sonderlösungen, die man leicht erraten kann.
Danach Polynomdivision.
Funktioniert in Deinem Fall NICHT -> falsch abgeschrieben oder ausgedacht?
b) Lese Wikipedia Bisektion. Man kann sich durch Probieren und Bereichshalbierung beliebig genau herantasten.
c) Newton-Verfahren (auch unter Wiki): auch numerisch wie b, jedoch weniger Schritte bei gleicher Genauigkeit
d) Telschritt & Cardanische Formeln (Vorstufe der exakten Formel, jedoch noch mit Fallunterscheidung
e) exakte explizite Lösungsformel: PQRSTUVW (analog zur pq-Formel nur einsetzen) -> jedoch mit komplexen Zwischenergebnissen. Komplett ausgeschrieben sind diese Formeln pro x (denn ein Polynom vom Grad 4 hat immer 4 Lösungen; manche komplex) über 330 Zeichen lang:
http://www.lamprechts.de/gerd/php/gleichung-6-grades.php
rechnet d) und e) online vor:
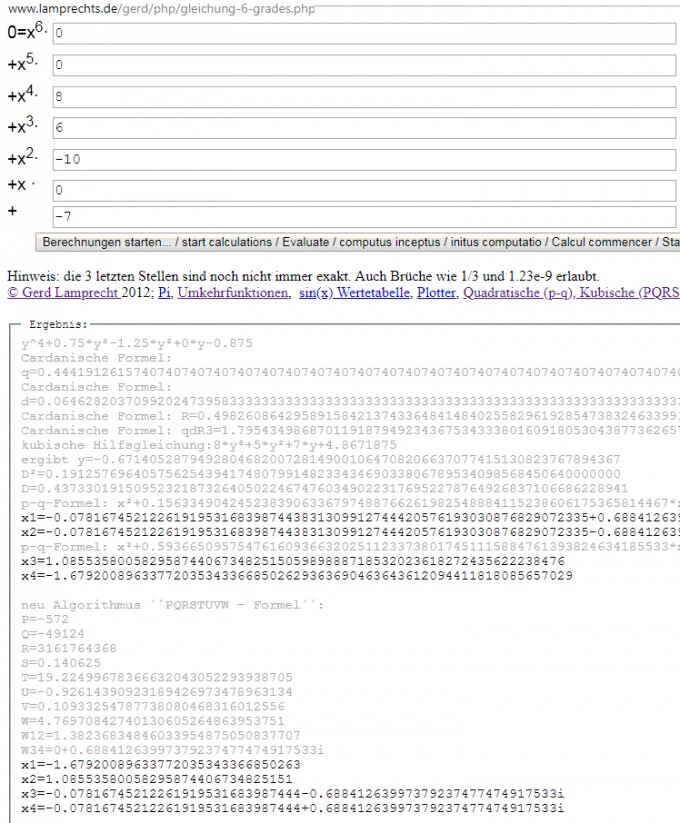
Interessant: wenn man mehr als 10000 Nachkommastellen berechnen will, wird c) schneller als die exakte lange explizite Formel von e), da Wurzeln auch iterativ berechnet werden müssen!
GTR rechnen nur wenige Nachkommastellen (meist weniger als 11) per b) und/oder c).