Integral: Aufgabe 2) d Integral 3 Funktionen. Für t>0 schliessen der Graph von ft , die Ortskurve seiner Extrempunkte...

Question

Hilfe- bislang wurde mir bereits ein Mal auf die Sprünge geholfen. Nun hab ich eine weitere Stolperfalle entdeckt die sich in der Aufgabe 4 ( siehe Anhang befindet)

2) d) Für t>0 schliessen der Graph von ft , die Ortskurve seiner Extrempunkte mit y=1,5x - 0.5 sowie...

Ich lese aus der Aufgabe heraus dass ein Integral dieser 3 gegebenen Funktionen gebildet werden muss, nun wo sind den die Integrationsgrenzen, sowie das Verfahren bei solchen Aufgaben. Bitte um ausführliche Erklärung 

Comments

Nun hab ich eine weitere Stolperfalle entdeckt
die sich in der Aufgabe 4
( siehe Anhang befindet)

Ist das Foto korrekt ?

Answer 1

ich nehme an, mit A4  meinst du 2d)

für t = 2 sieht das Ganze z.B. so aus:

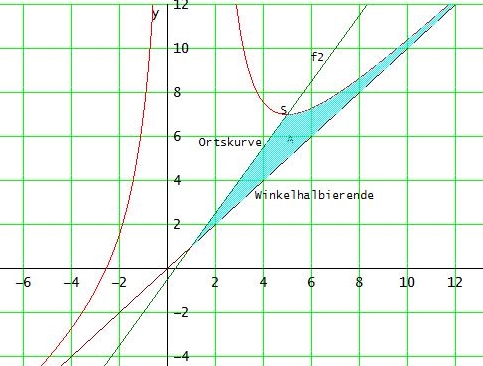
Du musst die Schnittstellen der Ortskurve mit der Winkelhalbierenden [ x_w ]

und mit f_t (x)  [ x_s ]  ausrechnen.

\(A_t=\int_{x_W}^{x_S} \! \text{ }(1,5x-0,5 - x) \, dx + \int_{x_S}^{∞} \! \text{ }(f_t(x)-x) \, dx \)

Beim zweiten Integral kannst du die obere Grenze erst einmal z nennen und am Schluss z→∞ betrachten.

Gruß Wolfgang

Comments

SUPER GEILE COMUNITY!!! VIELEN LIEBEN DANK WOLFGANG!!

Daraus entnehmen ich, dass die obere grenze des ersten Integrals die Schnittstelle zwischen ft(x) und der Ortskurve ist??

Lieben Gruß

Leontin

---

ja, so ist es,

und immer wieder gern :-)

---

echt Klasse! :)