Kreisberührungspunkt ?

Question

Hallo kann mir jemand helfen, wie ich da vorgehen muss?

Gegeben ist die Gleichung x^2+y^2=100 eines Kreises k und die Gerade g mit der Gleichung y= (Wurzel von 3)*x +n. Für welche Werte von n berührt die Gerade g den Kreis k?

Answer 1

Setze y = √3·x + n in die Gleichung x² + y² = 100 ein. Du bekommst dadurch eine quadratische Gleichung. Die Gerade g berührt genau dann den Kreis k, wenn die Gleichung eine einzige Lösung für x hat.

Comments

sorry für die blöde frage aber wenn ich es einsetzte bekomme ich:

4x^2 + 3.464xn+n^2-100=0

wie setzt ich das dann in die mitternachtsformel ein? lass ich die 100 auf der anderen seite?

---

wie setzt ich das dann in die mitternachtsformel ein?

a = 4

b = 2√3·n

c = n² -100

Die Mitternachtsformel für sich genommen ist (so wie jede Formel) nutzlos.

Eine Nutzen bekommt man erst dadurch, dass man auch weiß, wozu sie angewendet wird. Und zwar nicht nur schemenhaft a la "um quadratische Gleichungen zu lösen", sondern konkret um Gleichungen der Form

        ax² + bx + c = 0

zu lösen.

lass ich die 100 auf der anderen seite?

Ich hoffe du kannst dir die Frage jetzt selbst beantworten.

---

dann komm ich au -8.65+/- wurzel von -n^2 und das kann ich ja nicht mehr weiter rechnen oder?

oder kann ich mal -1 rechnen

sorrry..

---

dann komm ich au -8.65+/- wurzel von -n²

Dann hast du falsch eingesetzt oder falsch umgeformt.

\(x_{1,2} = \frac{-b\pm\sqrt{b^2-4ac}}{2a}=\frac{-2\sqrt{3}n\pm\sqrt{(2\sqrt{3}n)^2-4\cdot4(n^2-100)}}{2\cdot4}\)

Answer 2

Die Gerade schneidet die x-Achse im Winkel von 60°. Wenn A und B die Berührpunkte sind, dann schneitet AB die x-Achse im Winkel von 150° und die Gleichung von AB lautet y=tan(150°)·x oder y=-x/√3. Setze dies in die Kreisgleichung ein und löse nach x auf.

Comments

dann wäre die lösungen +/- 8.66? wie bist su auf -x/wurzel 3 gekommen?

---

tan(60°)=√3. Lass die Wurzeln so lange, wie möglich stehen.

Answer 3

Hier die Standardmethode zur Berechnung

Gegeben ist die Gleichung x^2+y^2 = 100 eines Kreises k und die Gerade g mit der Gleichung y= (Wurzel von 3)*x +n. Für welche Werte von n berührt die Gerade g den Kreis k?

Kreis
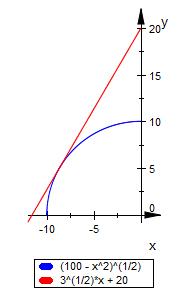
f ( x ) = √ ( 100 - x^2 ) = ( 100 - x^2 ) ^{1/2}
f ´( x ) = 1/2 * ( 100 - x^2 ) ^{-1/2} * (-2x)
f ´( x ) = - x * ( 100 - x^2 ) ^{-1/2}
Gerade
g ( x ) = √ 3 * x + n
g ´( x ) = √ 3

Definition Berührpunkt
f ( x ) = g ( x ) .| Koordinaten gleich
f ´ ( x ) = g ´ ( x ) | Steigung gleich

- x * ( 100 - x^2 ) ^{-1/2} =  √ 3
x = -5 * √ 3
in f ( x ) einsetzen
5
(  -5 * √ 3 | 5 )

g ( x ) = √ 3 * (-5 * √ 3 ) + n = 5
n = 20

g ( x ) = √ 3 * x + 20

Hinweis
Es gibt noch einen weiteren Punkt

Comments

ohh jee ich checks nicht.. danke aber trotzdem für eure hilfe..

---

Elementar :

m_(g)  =  √3  =  MY_(0) / MX_(0)  =  tan α  =  tan β  =  BY_(0) / BM

⇒  BY_(0)  =  BM·√3  =  10·√3

⇒  n = MY_(0)  =  √( (BY_(0)^2 + BM^2 )  =  √ (100·3 + 100)  =  20

(Mit arctan √3  =  60°  ⇒  γ = 30°  und sin 30° = 1/2 = MB / MY_(0)  geht es noch schneller.) 

---

in der Trigo aso alles was mit sin, cos ect zu tun hat, bin ich noch schlechter... -.-