As Spiegelmatrix bestimmen

Question

Wie die meisten von euch habe ich jetzt bald eine MatheKlasur.

Ich arbeite schon seit Stunden an dieser Aufgabe und konnte bei a) nur zur hälfte lösen. Könntet ihr mir den Lösungsweg mitgeben?

Die Fragen:

Gegeben sei m R^2 die Spiegelung S an der Geraden g gegeben durch 2x + 3y = 0

a) Geben Sie die vier Einträge der zu S gehörenden SpiegelMatrix As an.`

Answer 1

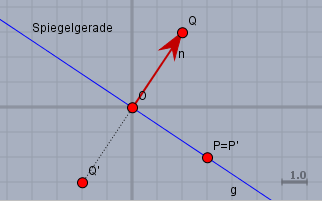
wenn Du die Spiegelmatrix \(A_S\) kennen würdest, so könntest Du mit ihr die Bildpunkte der Spiegelung berechnen. Du weißt, dass Punkte auf der Spiegelgeraden auf sich selbst abgebildet werden. So wie z.B. \(P=(3|-2)^T\) auf dem Bild

also ist

$$A_S \cdot \begin{pmatrix} 3 \\ -2 \end{pmatrix} = \begin{pmatrix} 3 \\ -2 \end{pmatrix}$$

Wohingegen ein Punkt \(Q\), der von Ursprung aus in Normalenrichtung der Spiegelgeraden verschoben wird, auf seine Negation abgebildet wird.

$$A_S \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} = \begin{pmatrix} -2 \\ -3 \end{pmatrix}$$

Zusammengefasst kann man auch schreiben

$$A_S \cdot \begin{pmatrix} 3 & 2 \\ -2 & 3 \end{pmatrix} = \begin{pmatrix} 3 & -2\\ -2 & -3 \end{pmatrix}$$ bzw.:

$$\begin{aligned} A_S &= \begin{pmatrix} 3 & -2\\ -2 & -3 \end{pmatrix} \cdot \begin{pmatrix} 3 & 2 \\ -2 & 3 \end{pmatrix}^{-1} \\ &=  \begin{pmatrix} 3 & -2\\ -2 & -3 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\ 2 & 3 \end{pmatrix} \frac{1}{13} \\ &= \frac{1}{13}\begin{pmatrix}5& -12\\ -12& -5\end{pmatrix}\end{aligned}$$

Noch ein Tipp: berechne mal die Eigenvektoren von \(A_S\).