Morgen steht die Klausur an und ich verstehe einfach nichts! Daher bitte ich euch um Hilfe:
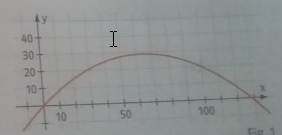
Der Flug eines Golfballes kann näherungsweise durch eine Parabel modelliert werden. Der Graph ist in der Figur abgebildet.
a) Begründe, ob die Flugbahn durch die Funktionsgleichung y1 = -0,007 x² + 0,9x; durch y2 = 0,007x² + 0,9x oder durch y3 = -0,07x beschrieben werden kann.
b) Gib die maximale Höhe des Fluges an.
c) Fliegt ein Ball, dessen Flugbahn durch die Punkte P(0|0), Q(10|10,3) und R(20|19,2) geht, höher bzw. weiter als der oben beschriebene Golfball? Begründe deine Antwort.