Deine Aussage
1+2sin(2t+pi) = k*pi
würde auf alle Stellen zutreffen beiden denen
die Funktionswerte übereinstimmen und nicht
nur 0.
Es soll aber
1+2sin(2t+pi)= 0 sein
2 * sin(2t+pi) = -1
sin(2t + π) = -1/2
2t + π = arcsin(-1/2)
2t + π = -0.5236
t = -1.833
Hier der Graph
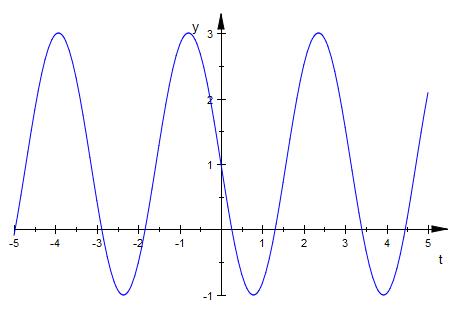 Was könnte man weiter machen ?
Was könnte man weiter machen ?
Den Abstand von x = -1.833 zum nächsten Hoch-
und Tiefpunkt bestimmen.
Die Funktion ist achsensymmetrisch dazu.
Und dann über diese Werte eine Funktion
der Nullstellen entwickeln.
mein Matheprogramm meint
0.262 * k * π
und
1.309 * k * π
k aus den ganzen Zahlen
Bin gern noch weiter behilflich.