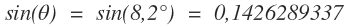ich stehe vor einem Problem undzwar bin ich momentan beim Tipler auf der Seite 1405 Kapitel Trigonometrie und Vektoren bei der Aufgabe 41.20 die da lautet: "Berechnen Sie sin(Tetha) für Tetha = 8,2°. Können Sie bei diesem Winkel die Kleinwinkelannäherung (sin(Theta)) gerundet Theta anwenden ? " Ich habe mir die Kleinwinkelannäherung angeschaut und da steht im Tipler wenn der Winkel klein ist gilt für den Bogenmaß Theta = s/c s steht für die Strecke glaub ich und die Winkelfunktionen sin(Theta) = a/c bzw. tan(Theta) = a/b näherungsweise gleich. Also den sin von 8,2 habe ich bereits ausgerechnet und da komme ich auf 0,14262. Jetzt habe ich mir die Kleinwinkelannäherung durchgelesen und kann damit irgendwie so rein gar nichts mit anfangen. Also gelesen und verstanden habe ich es ja aber irgendwie in die Praxis umsetzen geht irgendwie nicht. Achja und laut Lösung soll da 0,1431 rad raus kommen. rad steht ja für radiant.
Vielleicht kann mir das ma jemand anhand einer Beispiel Rechnung veranschaulichen.
VG :)
für den Bogenmaß Theta
Wandle Theta in Bogenmaß um.
s steht für die Strecke glaub ich
Finde heraus wofür s steht.
Hab ma was gefunden bin mir aber nicht sicher ob das die Kleinwinkelnäherung ist.
Also das steht im Buch.
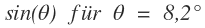
Wenn ich 8,2° im Bogenmaß umwandel, dann wäre das doch wie folgt oder:
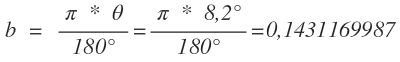
Aber was hat das jetzt mit einer Annäherung zu tun hmm :/
Mit dem Sinus komm ich auf das hier.
Wenn ich 8,2° im Bogenmaß umwandel, dann wäre das doch wie folgt
Krasser Scheß, das ist ja fast das gleiche wie sin(8,2°).
Ja das finde ich auch :D
Aus der Aufgabe geht doch hervor ob man die Kleinwinkelnäherung anwenden kann ? Woran erkenne ich denn allgemein jetzt wann die Kleinwinkelnäherung anwendbar ist oder halt nicht.
Also laut Bogenmaß und sinus funktion sind beide Ergebnisse sehr ähnlich bis ab der dritten Nachkommastelle.
Woran erkenne ich denn allgemein jetzt wann die Kleinwinkelnäherung anwendbar ist oder halt nicht.
Daran, dass der Fehler vernachlässigbar klein ist. Wo da die Grenze ist, kommt auf den Sachzusammenhang an. Der Fehler wird umso größer, je größer der Winkel ist. Bei 10° beträgt der Fehler ungefähr 0,5%.
im Buch ist eine Abbildung zu sehen im Tipler auf Seite 1407. Da steht direkt auf der horizontalen Achse Tetha in grad und direkt da drunter noch eine Skala Tetha in rad. Unter 10 Grad(Tetha) ist 0,2 rad.
Wie groß wäre denn in der oben genannten Problemstellung der Fehler und gibt es dazu evt. eine Formel ?
Der relative Fehler beträgt (θ/sin(θ) - 1).
In obigem Fall ergibt das
((8.2·π/180) / sin(8.2·π/180) - 1) ≈ 0.0034 = 0,34%.
Gleich mal was dazu gelernt. Top
VD und VG :)
k π/10k sin(π/10k) Unterschied1 0.3141 0.3090 0.00512 0.1570 0.15643 0.000643 0.10471 0.10452 0.000194 0.078539 0.078459 0.0000805 0.062831 0.062790 0,0000416 0.0523598 0.0523359 0.00002397 0.0448798 0.0448648 0.00001508 0.0392699 0.0392598 0.00001019 0.0349065 0.0348995 0.000007010 0.03141592 0.03141075 0.00000517
Ein anderes Problem?
Willkommen bei der Mathelounge! Stell deine Frage einfach und kostenlos
