§1: Wenn ein Produkt 0 werden soll, ist ein konstanter Faktor irrelevant ("Satz vom Nullprodukt")
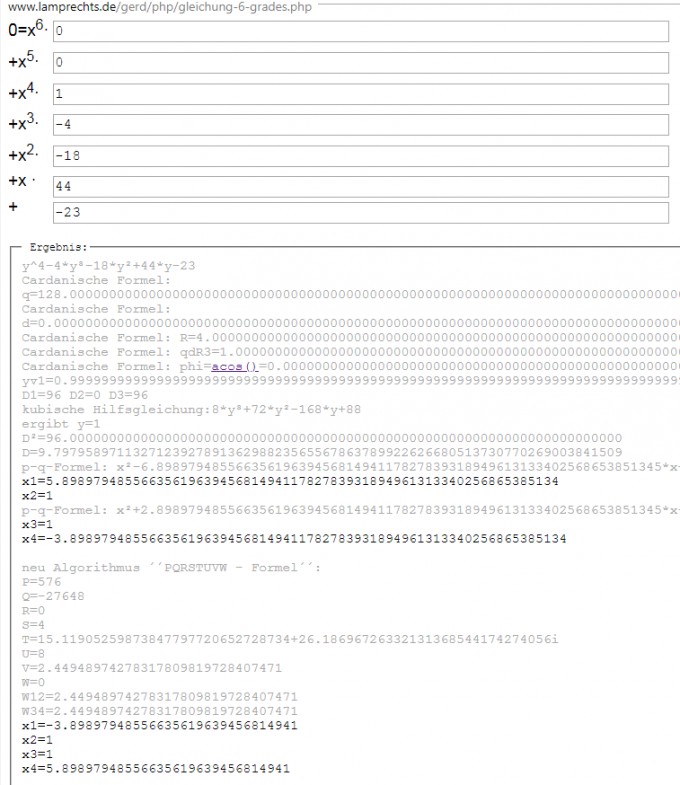
Aufgabe lautet also x^4-4x^3-18x^2+44x-23=0
§2: Da Lehrer ihren Schülern universelle Lösungswege bei Polynomen nur bis zum Grad 2 zumuten (p-q-Formel oder abc-Formel), werden höhere Grade nur Spezialaufgaben gestellt, die leicht zu erraten sind. Danach Polynomdivision, was zu (x - 1)² * (x² - 2*x - 23) = 0
führt.
Manchmal gibt es auch Spezialfall-Aufgaben, wo nur geradzahlige Potenzen vorkommen, die dann per Substitution lösbar sind (z=x² -> ergibt pq-Formel für die z-Gleichung)
a) Geschichtlich gesehen kam bei universellen Lösungswegen (frei von Spezialfällen) vor etwa 1000 Jahren die Bisektion.
(https://de.wikipedia.org/wiki/Bisektion )
b) Mindestens 500 Jahre ist https://de.wikipedia.org/wiki/Newton-Verfahren bekannt.
c) Mindestens 200 Jahre kennt man https://de.wikipedia.org/wiki/Cardanische_Formeln
(noch mit Fallunterscheidung & trigonometrischen Funktionen)
d) Etwa 100 Jahre kennt man die aus c) optimierten expliziten PQRSTUVW Formeln.
http://www.lamprechts.de/gerd/php/gleichung-6-grades.php
rechnet c) und d) vor: