
Ich habe bisher
a) surjektiv da es zwei verschiedene y nach den gleichen x => nicht injektiv => surjektiv (EDIT: Ich habe eigentlich getestet und es ist auch nicht surjective. Ich glaubte dass nicht injektiv => surjektiv und umgekehrt aber dass stimmt hier nicht. Dann was bedeuted es wenn es nichr sur. und nicht inj. ist? Ich glaubte das alle funk sind entweder sur, inj oder bijektiv.
b)injektivität habe ich gezeigt mit beliebige x1,x2 von f(x1)=f(x2) => x1=x2
aber beim surjektivität: wobei die definition lautet 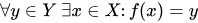 bekomme ich x=√y wobei,
bekomme ich x=√y wobei,
für negative y, x=√y soll auf der Komplexemenge liegen. Bedeutet das, dass es nur injektiv ist?
c) surjective
d) bijektiv