Ableiten und zusammenfassen.
Bsp. f(x) = x^5 * e^{3x} + 1
f '(x) = ( x^5 * e^{3x} )' + (1 )'
f '(x) = ( x^5 * e^{3x} )' +0
f '(x) = ( x^5 * e^{3x} )' . Produkt aus u(x) = x^5 und v(x) = e^{3x}
Nebenrechnung
u(x) = x^5 , u ' (x) = 5 * x^4
und v(x) = e^{3x}, v' (x) = 3 * e^{3x}
f '(x) = ( x^5 * e^{3x} )' | Produktregel ( u * v)' = u' * v + u * v'
= 5x^4 * e^{3x} + x^5 * 3 * e^{3x} | e^{3x} ausklammern
= ( 5 x^4 + 3 x^5 ) * e^{3x} | x^4 ausklammern
= x^4 (5 + 3x) * e^{3x}
Eine der beiden letzten Zeilen kannst du dann stehen lassen.
Kontrolle mit wolframalpha.com
https://www.wolframalpha.com/input/?i=f(x)+%3D+x%5E5+*+e%5E(3x)+%2B+1
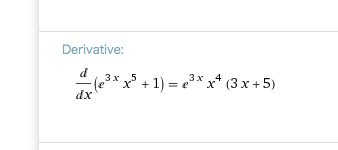
Auf die Ableitung f '(x) kannst du klicken. Dann hast du dort eine "alternate form" und weitere Informationen zur ersten Ableitung von f(x) .
