Mal ein paar Vorbemerkungen:
Die Richtungsangaben mache ich lieber mit sin/cos, Weil dabei automatisch ein Richtungsvektor der Länge 1 entsteht. Da tun wir uns leichter die Geschwindigkeit einzuarbeiten - oder Du normierst die Richtungsvektoren.
Die Geschwindigkeiten rechne ich im km/s um, weil relativ kurze Zeitabstände zu betrachten sind. Die Koordinaten sind wohl im km zu sehen.
\(v1_{kms} = 800 / 3600= 2/9\)
\(v2_{kms} = 600 / 3600 =1/6\)
damit (t in Sekunden)
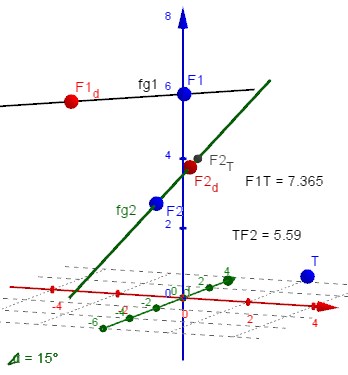
\(fg1(t) \, := \, \left(-2, 5, 5 \right) - t \; \left(\operatorname{sin} \left( 45^{\circ} \right), \operatorname{cos} \left( 45^{\circ} \right), 0 \right) \; \frac{2}{9}\)
\(fg2(t) \, := \, \left(0, -2, 3 \right) + t \; \left(0, \operatorname{cos} \left( 15^{\circ} \right), \operatorname{sin} \left( 15^{\circ} \right) \right) \; \frac{1}{6}\)
zum Zeitpunkt t_0 fliegt die eine Maschine nach Norden und die andere nach Süd-Westen, weil sie sich im gleichen Zeitfenster "aufeinanderzubewegen" bewegt sich f2 mit "positivem" und f1 mit "negativem" Richtungsvektor.
Wenn Du damit weiter machen willst dann sag Bescheid...