Hallo Chingo,
leider kein Plan ?
zumindest solltest Du Dir eine Zeichnung machen. So eine wie diese:
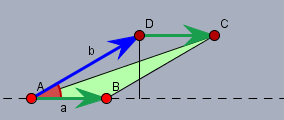
Dort siehst Du den (grünen) Vektor \(\vec{a}\) mit der Länge \( \| \vec{a} \| = 3\) und den (blauen) Vektor \(\vec{b}\) mit der Länge \(\|\vec{b}\| = 5\). Der Winkel (rot) zwischen beiden Winkeln beträgt 30°. Gefragt ist nun nach einem Dreieck was durch \(\vec{a}\) und \(\vec{a} + \vec{b}\) aufgespannt wird. Den Vektor \(\vec{a} + \vec{b}\) bilde ich, indem ich den Vektor \(\vec{a}\) einfach nochmal an \(\vec{b}\) anhänge. Die Reihenfolge spielt bei der Addition von Vektoren keine Rolle. D.h. der Vektor \(\vec{a} + \vec{b}\) ist nun der Vektor von \(A\) nach \(C\) in der Zeichnung.
Die Fläche \(F\) des grünen Dreiecks \(\triangle ABC\) ist wie bei allen Dreiecken $$F = \frac12 h g$$ Die Grundseite \(g\) ist hier \(g=|AB| = \|\vec{a}\| = 3\) und die Höhe \(h\) (schwarz) ist $$h = \|\vec{b}\| \cdot \sin(30°) = 5 \cdot \frac12$$ Macht dann $$F = \frac12 hg = \frac12 \cdot 5 \cdot \frac12 \cdot 3 = 3,75$$ Vielleicht fällt Dir auf, dass es für die Berechnung der Fläche völlig egal ist, ob das Dreieck durch \(\vec{a}, \vec{a}+\vec{b}\) oder einfach durch \(\vec{a}, \vec{b}\) gebildet wird. Falls irgendetwas unklar ist, so frage bitte nach.
Gruß Werner