Hallo Chingo,
zeichnen ist immer gut und in diesem Falle besonders gut. Ein Quadrat \(PQRS\) existiert so gar nicht. Wenn schon, dann ist ein Quadrat \(PRSQ\) möglich. Vierecke im besonderen und Polygone im Allgemeinen werden so bezeichnet, dass die Punkte im mathematisch positivem Sinn umlaufend bezeichnet werden. Und das ist hier nicht der Fall - ansonsten müsste der Winkel \(\angle RQP\) (blau) ein rechter sein. Das ist er aber nicht. Eine Skizze bringt es an den Tag.
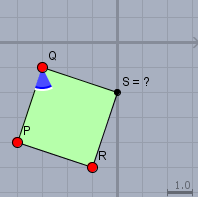
Aus der Skizze kann man die Koordinaten vom Punkt \(S\) direkt ablesen $$S = \begin{pmatrix} 0\\-2 \end{pmatrix}$$ wenn man (aus der Skizze!) weiß, dass \(QR\) die Diagonale bildet, so kann man den Punkt \(S\) auch berechnen: $$S = Q +R - P \\ \quad = \begin{pmatrix}-3\\-1 \end{pmatrix} + \begin{pmatrix} -1\\-5 \end{pmatrix} - \begin{pmatrix} -4\\-4 \end{pmatrix} \\ \quad = \begin{pmatrix} -3 - 1 +4\\-1 - 5 +4 \end{pmatrix} \\ \quad = \begin{pmatrix} 0\\-2 \end{pmatrix}$$ Gruß Werner