ich stehe vor folgendem Problem.
Ich habe eine Ellipse in der x-y-Ebene im R^3 in der Form
$$ E=\begin{pmatrix}a\cdot \cos(\varphi)\\ b\cdot \sin(\varphi)\\0\end{pmatrix} $$
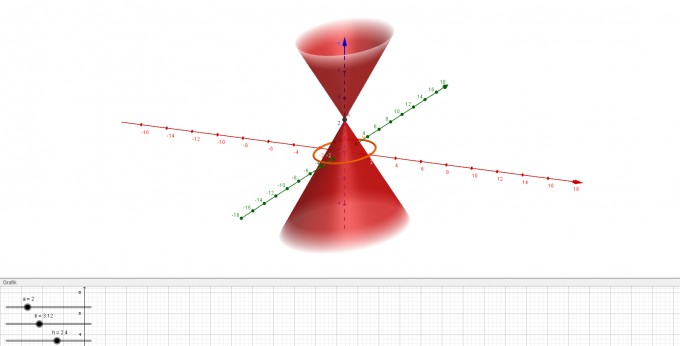
vorliegen. Dies soll die Schnittkurve (Orange) von Grundfläche und Mantelfläche sein.
Die Spitze wird in z-Richtung durch den Punkt (0,0,h) beschrieben.
Die Koordinatengleichung für einen elliptischen Kegel lautet nach Wikipedia:
$$ K_{a,b}: \frac{x^2}{a^2}+\frac{x^2}{b^2}=z^2,\quad a,b>0 $$
https://de.wikipedia.org/wiki/Kegel_(Geometrie)
Dieser hat die Spitze im Koordinatenursprung (0,0,0).
Jetzt zum Problem:
Ich will nun diese Gleichung so abändern, sodass die Spitze im Punkt (0,0,h) liegt und die Schnittkurve E (Orange) enthält. Meine bisherige Idee war nun zunächst die z-Komponnete so zu modifizieren, sodass ich erstmal diese Form von Gleichung bekomme:
$$ K_{a,b}: \frac{x^2}{a^2}+\frac{x^2}{b^2}=(z-h)^2 $$
Allerdings bekomme ich hier stark Probleme, weil wenn ich die Parameter a,b,h verändere, dann ist zwar die Spitze immer in dieser Menge enthalten, aber nicht die Schnittkurve. Mein erster Gedanke war nun eine neue Konstante c einzuführen mit c*(z-h)^2, um diese unerwünschten Ausbrechungen zu vermeiden. Das scheint sich aber auch als schwierig zu erweisen. Was mache ich falsch???