1. f ist injektiv:
f muss injektiv sein, weil g sonst keine Umkehrfunktion sein könnte.
2. f ist surjektiv
f muss nicht surjektiv sein. Es kann auch Elemente in Y geben die kein Urbild haben.
3. g ist injektiv
Meiner Meinung nach braucht g nicht injektiv zu sein.
4. g ist surjektiv
g muss surjektiv sein, damit jedes Element aus X ein Urbild erhält. Sonst würde die Umkehrfunktion nicht für alle x gelten.
5. Es gilt (g o f ) (y)= (y) für alle y Element aus Y.
f ist definiert als Funktion aus X nach Y. Daher gilt sie für alle Elemente aus X nicht aber für alle Elemente aus Y.
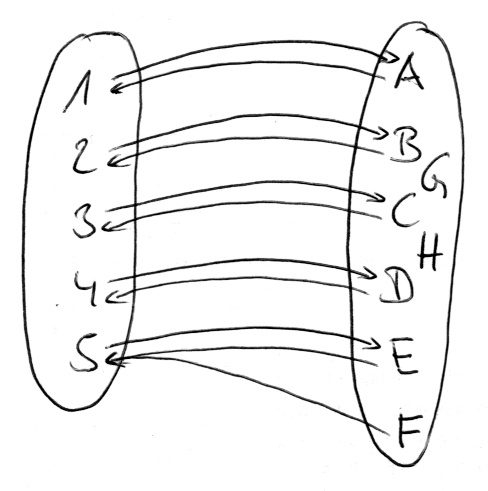
Hier eine kurze Skizze wie ich es mir vorstelle.