Hilfe bei folgender Aufgabe!
An einem weihnachtlichen Fenster wächst eine Eisblume nach folgendem rekursiven Bildungsgesetz: Die Ausgangsfigur T₀ ist ein gleichseitiges Dreieck mit der
Kantenlänge 1. Die Berandung von Tn+1 entsteht aus der von Tn, indem auf dem mittleren Drittel einer jeden geradlinigen Berandungsstrecke von Tn ein gleichseitiges Dreieck aufgestzt wird.
Man berechne den Umfang Un und den Flächeninhalt Fn von Tn und zeige:
\( \lim\limits_{n\to\infty} \) Un = ∞, \( \lim\limits_{n\to\infty} \)Fn < ∞
(Durch den Grenzprozess n → ∞ erhält man ein fraktales Gebilde, bei dem die
Umrandungskurve in keinem Punkt eine Tangente besitzt.)
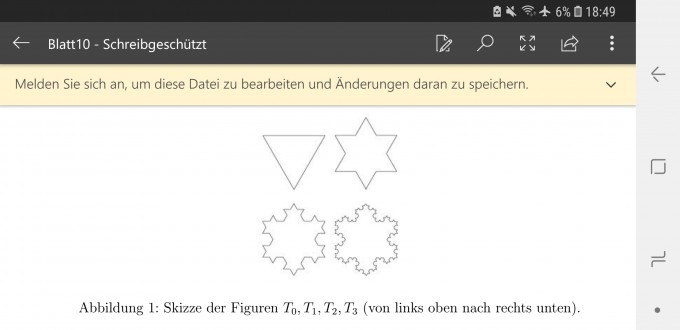
Zu der Aufgabe gibt es eine Abbildung zu den Skizzen der Figuren, welche ich mit hochgeladen habe: