Für was sollen das denn die Grenzen sein? für x oder y? du musst doch vom unteren Rand des Gebietes zum oberen integrieren und dann von links nach rechts. richtig ist dass die Schnittpunkt bei x=-1 und x=+1 liegen.
Hast du denn schon irgendwann mal mit einem Doppelintegral eine andere Fläche als Rechtecke ausgerechnet? Ihr müsst doch mindestens ein Beispiel haben?
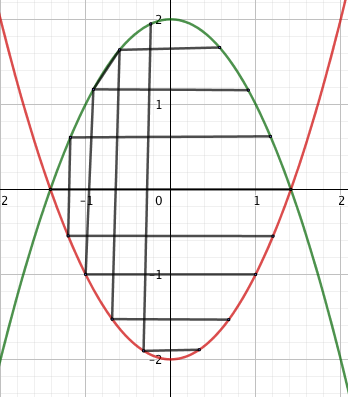
Zur Vorstellung: du teilst dir das Gebiet in Streifen der Breite Δx ein, diese wiederum in Rechtecke der Breite Δy. Dann addierst du von unten angefangen alle Rechtecke in einem Streifen, der bei der unteren Kurve, bei dir -x^2 anfängt und bei der oberen aufhört , ich hab das mal ein Stück weit für das Gebiet zwischen x^2-2 und -x^2+2 gezeichnet, wenn man die Rechtecke immer kleiner macht ist ein Streifen dann \( \int\limits_{x^2-2}^{-x^2+2} dy*dx\) dann musst du noch alle Streifen hier von \( -\sqrt{2} \) bis \( +\sqrt{2} \) summieren und hast insgesamt:
\( \int\limits_{- \sqrt{2} }^{ \sqrt{2} } \int\limits_{x^2-2}^{-x^2+2} dy*dx\)