Vom Duplikat:
Titel: Planimetrie - Sektor Flächeninhalt/Umfang berechnen?
Stichworte: geometrie,kreis,dreieck,umfang,flächeninhalt
Kurze Worte:
Leider komme ich nicht ganz auf die Lösung und wir haben keine Lösungswege erhalten sondern nur das Resultat... Bitte schreibt auch den Lösungsweg hin
Meine Lösung:
Flächeninhalt vom EI -> A1 = r²π /2 + A▲ = habe ich 100% falsch + Asektor = (r√2)²π/4
Umfang vom EI -> U1 = 2rπ/2 + U▲ = 2r + 2(r√2) + U3 = weiss ich nicht
Aufgabe:
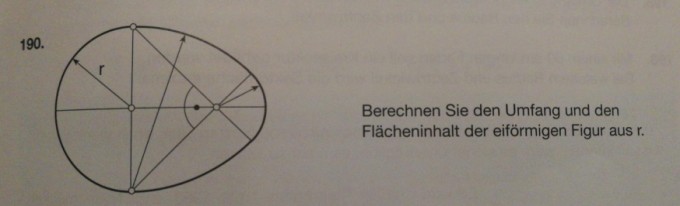
Hinter diesem Link findet ihr ein Bild zu der Aufgabe.
Lösung:
u = (3-√0.5)πr
A = (3π-π√2-1)r²
Wie kommt man auf diese Lösung ?