Wie berechnet man die Fläche dieses Fidget Spinners?

Question

Aufgabe:

Ich muss die schraffierte Fläche berechnen.

Problem/Ansatz:

Ich habe versucht die Stücke vom 6 Eck zu füllen von den Kreisen auszuschneiden, aber ich weiss nicht, ob das eine gute Idee wäre.

Comments

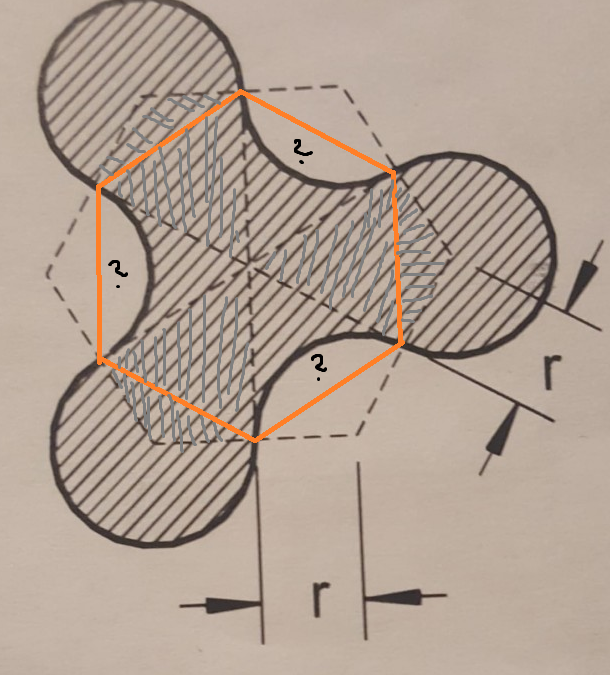
Die grauen Flächen konnte ich so berechnen: 3 * r^2 / 4 * Wurzel3 + 3* 3/4* r^2 * pi Da die Kreissegmente dort gleichschenklige Dreiecke sind, konnte ich den Anteil am Kreis berechnen.

Wie muss ich weiterrechnen?

Eigentlich bräuchte ich jetzt diese Fragezeichenflächen und könnte dann gleichseitiges Dreieck - Fragezeichefläche rechnen und hätte die Flächen dort auch noch. Dann noch die äusseren dazu addieren und das wäre alles.

Wie berechne ich die Fragezeichenflächen?

Answer 1

Das macht doch Sinn wie du es sagst.

Du könntest die Fläche des Sechsecks nehmen plus die darüber hinausgehenden Kreissegmente minus der darin liegenden Kreissegmente.

Willst du das mal probieren?

Ich glaube ich komme da auf eine Fläche von

A = r^2·(pi + 6·√3)

Comments

Wie meinst du das genau, könntest du mir vielleicht das ganze visualisieren?

---

Ich habe das so gemacht:

3/2r^2*Wurzel3 + 2r^2*pi - r^2*pi

Wieso funktioniert das nicht?

Ich verbinde eben die 6 oberen Kreisteile zu 2 ganzen Kreisen und ziehe dann noch die 3 Teile, welche einem Kreis entsprechen ab.

---

pi*r^2 habe ich ja auch wenn du mal hinschaust.

Deine Formel fürs 6eck scheint nur verkehrt zu sein.

---

Ich bin so blöd. Ich habe glaubs denn Fehler.

---

Ich habe es doch noch nicht richtig verstanden. Welche Segmente meinst du?

---

Ich meine zunächst einmal das Bereits eingezeichnete Sechseck. Dort ist die Seitenlänge 2*r. Das siehst du oder?

Dieses Sechseck berechnest du zunächst vom Flächeninhalt.

Dann musst du davon 3 mal einen Kreissektor mit einem Winkel von 120 Grad herausschneiden.

Dazu kommen dann 3 Kreissektoren mit einem Winkel von 240 Grad.

---

Woher kennst du den Winkel der Kreissektoren? Diese 240 Grad Winkel??

---

Zeichne dir mal in das Seckseck die Diagonalen ein, die durch den Mittelpunkt des Sechsecks gehen.

Du solltest 6 gleichseitige Dreiecke mit der Seitenlänge 2*r erhalten. Du weißt das jeder Winkel im gleichseitigen Dreick 60 Grad ist. Also z.B. die Innenwinkels des Secksecks somit 120 Grad betragen. Dann ist der Rest zum Vollwinkel noch 240 Grad.

---

Wie meinst du das mit dem Innenwinkel. Der Innenwinkel im gleichseitigen Dreieck ist doch 180 Grad?

---

Ich habe morgen eine Prüfung und der Lehrer hat angedeutet, dass ich mir diese Aufgabe sehr gut anschauen soll. Könnte mir jemand das bitte ganz genau erklären. Ich will das endlich verstehen.

---

Zeichne dir mal in das Seckseck die Diagonalen ein, die durch den Mittelpunkt des Sechsecks gehen.

(= im gestrichelten Sechseck)

Schreibe auch alle Winkel an, die du in den Dreiecken zwischen dem gelben und dem gestrichelten Sechseck findest.

---

Ich habe als Fläche für das Sechseck 6r^2Wurzel3 bekommen. Stimmt das?

---

Von welchem Sechseck sprichst du? Gestrichelt oder gelb?

---

Gestrichelt.

Ich habe das jetzt so gemacht:

6r^2Wurzel 3 - r^2*pi + 2r^2*pi. ..

---

Hier mal, was ich angeschrieben habe.

Ich denke du bist auf dem richtigen Weg. Forme mal dein Ergebnis um in das Ergebnis vom Mathecoach.

---

Ich habe es geschafft!

6r^2 Wurzel3-r^2*pi+2r^2*pi = r^2(6Wurzel3+pi)

---

Gut so! Zum gestrichelten Sechseck kommt im Prinzip einfach noch eine Kreisfläche dazu. Der Rest hebt sich gegenseitig auf.

---

Jetzt nur noch den blöden Umfang berechnen. :D

---

Wieviele Kreisumfänge sind das denn?

---

3 mal 2r^2 *pi von diesen drei Sektoren.

Dann noch die 3 innen Umfänge.

---

Schau dir nochmals meine Zeichnung an. Das Quadrat bei r^2 kann nicht stimmen. Umfang muss eine Längeneinheit keine Flächeneinheit haben.

[spoiler]

Vorschlag:

U = 3 * 2πr = 6πr

---

Habs geschafft!

2*r*pi* 2/3 * 3 = 4pi*r

2*r*pi * 1/3 * 3 = 2pi*r

4pi*r+2pi*r = 6pi*r

---

Prima. Herzlichen Glückwunsch.