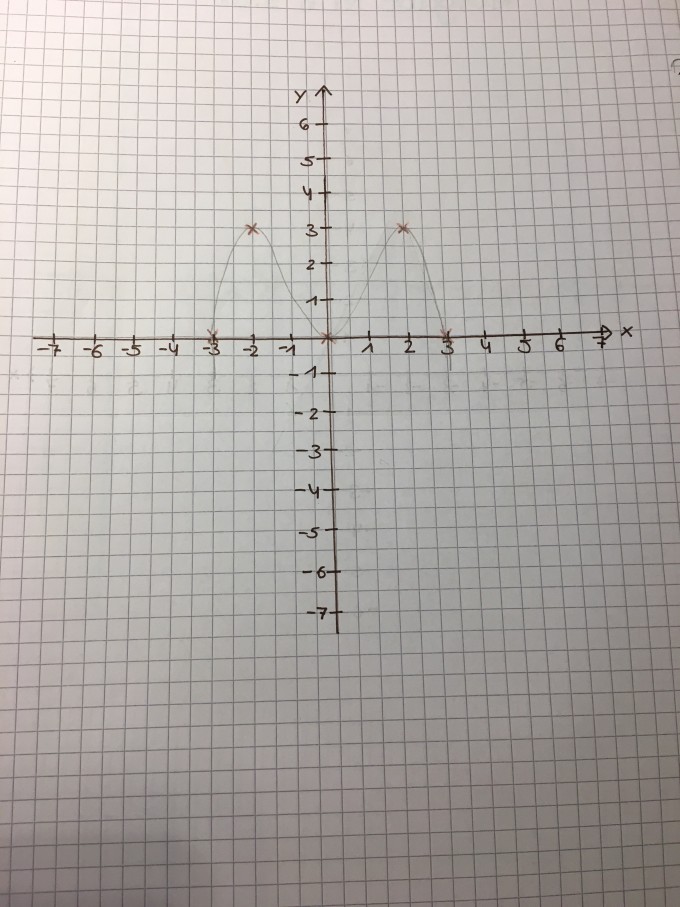Charakteristische Punkte eines Graphen (Zeichnen)

Question

Aufgabe:

Skizzieren Sie einen möglichen Graphen einer ganzrationalen Funktion mit den angegebenen Eigenschaften .Vergleichen Sie mit der Skizze Ihres Partners .Hat der Graph noch weitere charakteristische Punkte ? Wenn ja ,welche ?

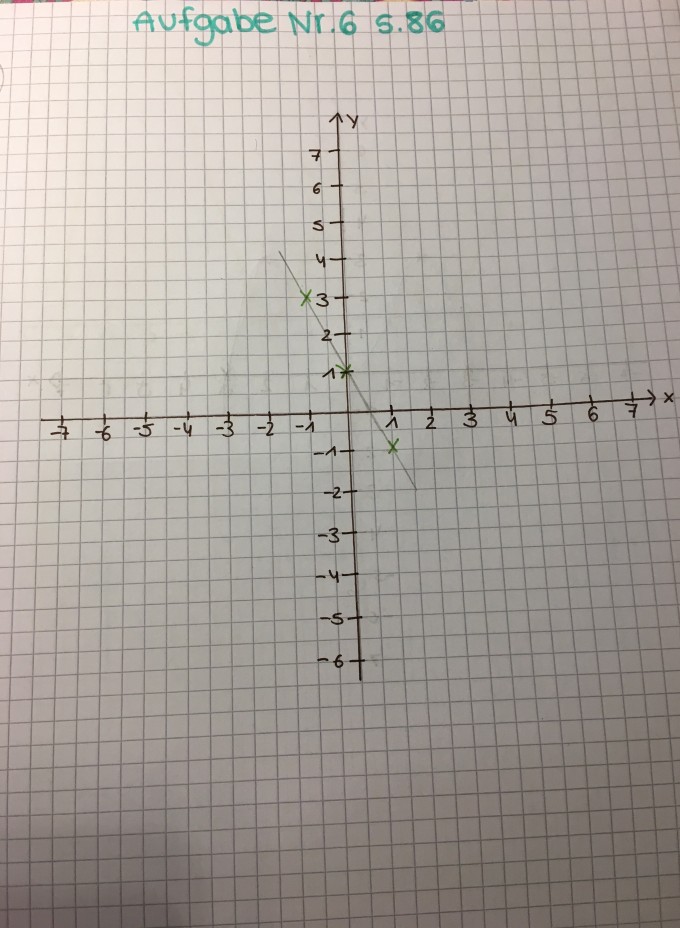
a) Achsenschnittpunkt S(0/1) und H (-1/3)  und Tiefpunkt T (1/-1)

b) Hochpunkt H1(-2/3) und H2 (2/3) sowie Nullstellen bei x1=-3 und x2=0 x3=3

Problem/Ansatz:

Wollte fragen, ob meine Zeichnungen richtig sind ?

Answer 1

ich habe ein wenig getrickst, denn ich habe die Funktionen rekonstruiert.

Der erste Graph könnte so aussehen:

Der zweite Graph könnte so aussehen:

Comments

An der Stelle x=2 hast du aber keinen Hochpunkt.

---

zweiter Graph:

Hochpunkt H1(-2/3) und H2 (2/3) sowie Nullstellen bei x1=-3 und x2=0 x3=3

???   H2 sollte wohl eher auch ein Hochpunkt sein

---

Habe eben die falsche Grafik angehängt, nun ist es richtig.

---

@LittleMix, ich empfehle dir einmal anzusehen, wie verschiedene Polynome mit unterschiedlichem Grad verlaufen. Dass du bei dem ersten Graphen eine lineare Funktion gezeichnet hast, zeugt davon, dass du kein Gefühlt dafür hast; das ist aber essentiell!

Answer 2

Die zweite Skizze sieht gut aus. Die erste nicht. Eine lineare Funktion hat keine Hoch- oder Tiefpunkte.

Answer 3

Dein zweiter Graph sieht richtig aus. Der erste weniger

Bei a) würde ich persönlich auch H als Hochpunkt interpretieren. Ansonsten würde man eher A vergeben. Letztendlich ist es aber egal wie man es interpretiert. Es gibt dann halt mehrere mögliche Kurvenverläufe.

~plot~ x^3-3x+1;0,0075x^6-0,2475x^4+1,62x^2 ~plot~