Bestimme zunächst \(P\) durch Einsetzen von \(x=4\) in die Geradengleichung von \(g\). Ergebnis ist \(P=(4/7)\).
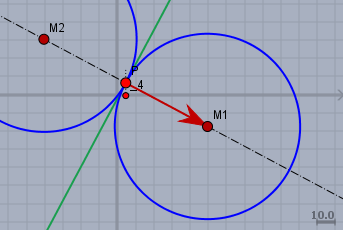
Um nun von \(P\) zum Mittelpunkt des Kreises zu kommen, benötigt man einen Vektor \(v\) (rot) der senkrecht auf der Geraden steht und die Länge \(51\) hat. Die Richtung dieses Vektors folgt bereits aus der Geradengleichung, wenn man sie in der Normalform schreibt. $$\begin{aligned} 15 x - 8y - 4 &= 0 \\ \begin{pmatrix} 15\\ -8 \end{pmatrix} \cdot \begin{pmatrix} x\\ y \end{pmatrix} - 4&= 0 && n = \begin{pmatrix} 15\\ -8 \end{pmatrix} \end{aligned}$$ Somit ist \(v\)$$v = \frac {51}{|n|} n = \frac{51}{\sqrt{15^2 + 8^2}} \begin{pmatrix} 15\\ -8 \end{pmatrix} = \begin{pmatrix} 45\\ -24 \end{pmatrix} $$Folglich liegt der Mittelpunkt \(M_1\) des Kreises bei$$M_1 = P + v = \begin{pmatrix} 4\\ 7 \end{pmatrix} + \begin{pmatrix} 45\\ -24 \end{pmatrix} = \begin{pmatrix} 49\\ -17 \end{pmatrix} $$Daraus folgt die Kreisgleichung $$(x-49)^2 + (y+17)^2 = 51^2$$Um den zweiten möglichen Mittelpunkt \(M_2\) zu berechnen, gehe von \(P\) aus in die Gegenrichtung: \(M_2 = P -v\)
