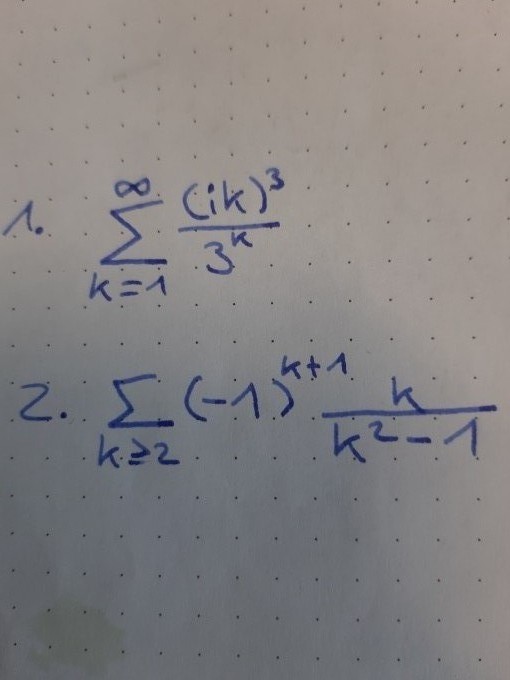Reihen sollen auf Konvergenz oder Divergenz untersucht werden?

Question

ich habe mich schon an die beiden Aufgaben, die ich jetzt reinstellen werde, gesetzt aber ich scheine immer auf verschiedene Ergebnisse zu kommen und würde gerne weitere Lösungsansätze hören.

Es sollen das Quotienten- und Leibnizkriterium enthalten sein.

Aufgabe:

Σ(ik)³/3^k , obere Grenze ist unendlich und k=1

∑(-1)^k+1(k/k² -1) , die obere Grenze ist nicht gegeben und k ≥ 2.

Comments

Wie lautet die Aufgabe? Soll auf Konvergenz untersucht werden?

---

Ja, auf Konvergenz oder Divergenz.

Answer 1

Zunächst lässt sich folgende Umformung vornehmen:

- i·\( \sum\limits_{k=1}^{\infty} \) (\( \frac{k^3}{3^k} \)).

\( \sum\limits_{k=1}^{n} \) (\( \frac{k^3}{3^k} \))=\( \frac{33}{8} \) - f(n)  mit \( \lim\limits_{n\to\infty} \) f(n)=0.

Also ist die Summe -\( \frac{33i}{8} \)

Comments

Bei 2. könnte Leibniz funktionieren.

---

Darf man die Variable i denn so vor die Sigma Notation stellen und dem k entnehmen?

Answer 2

die erste Reihe untersuchst du mit dem Quotientenkriterium, sie konvergiert. Die zweite Reihe mit Leibniz.

Sie verhält sich im wesentlichen wie die alternierende harm. Reihe, konvergiert also.

Comments

Welcher Leibni(t)z war das eigentlich? https://de.wikipedia.org/wiki/Gottfried_Wilhelm_Leibniz oder ...?

---

Ja, der wars. Habe mich verschrieben.

---

Vielen Dank! :)

---

(i·k)³=i³·k³=i²·i·k³= - i·k³. Jetzt darf man - i vor die Summe ziehen (ausklammern).

---

Achso, danke schön!

---

@jc2144: Danke für die Info. Das soll man anscheinend nicht so eng sehen. Gemäss Link hiess er Vater Leibnütz (Französische Version: Leibnitz) und dessen Sohn ab 1671 Leibniz.