Wie kann ich beweisen, dass der Winkel in einem Drachenviereck, welches in einem Umkreis eingeschlossen 90° ist?

Question

Miteinander

Wie kann ich beweisen, dass der Winkel in einem Drachenviereck, welches in einem Umkreis eingeschlossen 90° ist?

Aufgabe: Ein Kegel mit Radius r und Mantellinie s wird in eine Kugel eingeschrieben. Bestimmen Sie ihren Radius R.

a) mit r und s allgemein

Oder wie kann man diese Aufgabe sonst lösen?

In meinen Lösungen steht folgendes?

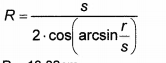
Ich habe folgende Lösung:

Vielen Dank im Voraus!

LG
AP2019

Answer 1

.. wie man auf diese Lösung kommt? $$R=\frac{s}{2 \cdot \cos \left( \arcsin \frac rs \right)}$$

Betrachte folgende Skizze:

Der blaue Winkel oben beim Punkt \(C\) sei \(\varphi\). In dem Dreieck \(\triangle APC\) ist $$\sin \varphi = \frac {r}{s}$$und in dem Dreieck \(\triangle QMC\) ist$$\cos \varphi = \frac {\frac s2}R = \frac {s}{2R}$$Löst man die erste Gleichung nach \(\varphi\) auf und setzt es in die zweite ein, so ist$$\cos\left( \arcsin \frac rs \right) = \frac {s}{2R} \\ \implies R=\frac{s}{2 \cdot \cos \left( \arcsin \frac rs \right)}$$Gruß Werner

Comments

@Werner: Schöne Antwort. Mach daraus doch auch noch eine eigenständige Antwort.

---

Mach daraus doch auch noch eine eigenständige Antwort.

wie? einfach nochmal kopieren oder gibt es einen Knopf, den ich noch nicht gesehen habe?

---

Du müsstest vermutlich kopieren. Ich kann auch umwandeln, wenn das einfacher ist (?)

Ich habe hier https://www.mathelounge.de einen Button "Kommentar zu Antwort". 

Ist nun erledigt. Zurückumwandeln kannst du ja selber wieder via "bearbeiten".

Answer 2

Ich habe den Rest ausgerechnet. Deine Formel ist um den Faktor 2 verkehrt.

Einfacher geht es mit den allgemeinen Formeln für rechtwinklige Dreiecke.

p = √(s^2 - r^2)

Dabei ist p die Höhe des Kegels.

q = r^2/p

R = 1/2·(p + q) = 1/2·(√(s^2 - r^2) + r^2/√(s^2 - r^2)) = s^2/(2·√(s^2 - r^2))

Also lautet die Formel

R = s^2/(2·√(s^2 - r^2))

Und hier braucht man keine blöden trigonometrischen Funktionen.

Comments

Danke vielmals Der_Mathecoach, Könnten Sie mir eventuell noch erklären wie man auf diese Lösung kommt?

---

Die angebliche Lösung kann man vereinfachen zur Antwort von mathecoach.

Diese Formeln https://de.wikipedia.org/wiki/Formelsammlung_Trigonometrie#Umrechnung_in_andere_trigonometrische_Funktionen

lassen sich praktisch alle mit den trigonometrischen Pythagoras herleiten. Versuche das, falls es wichtig ist, dass du das kannst. Studiere mal den Link und vergleiche mit eurer Theorie.

Answer 3

Hallo

denk dir das Drachenviereck an der langen Diagonalen halbiert, die muss der Durchmesser des Kreises sein, damit auch die 2 anderen Punkte auf dem Kreis liegen, müssen sie 90° sein (Thaleskreis)

den Rest hab ich nicht nachgerechnet.

Gruß lul