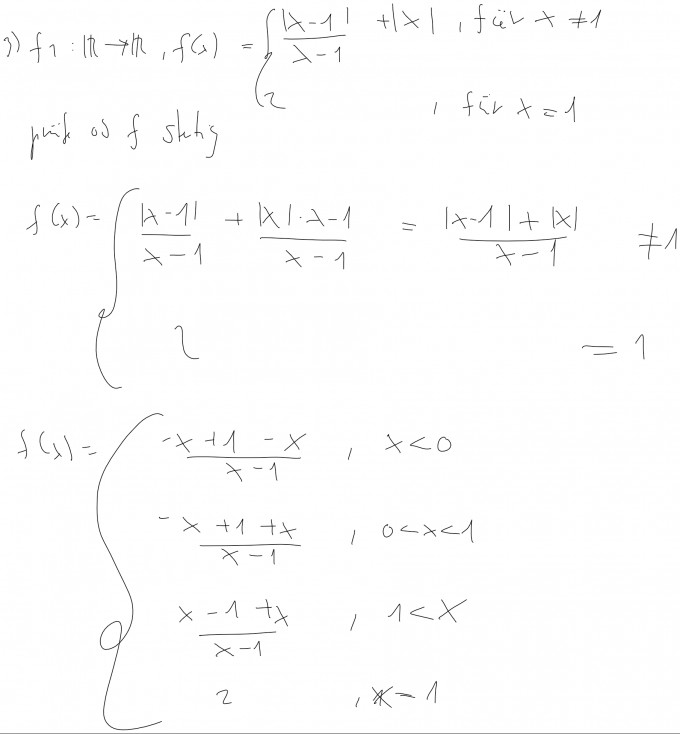Aufgabe:
habe keine Ahnung ob, das so richtig ist.
ich muss ja den Rechseitigen Grenzwert und den Linkseitigengrenzwert ausrechnen, nur das Problem ist, dass ich nicht verstehe wie ich die Beträge Sinnvoll auflösen soll.
da wenn ich x<1 für lGw und x>1 für rGw nicht stimmen kann weil da noch ein |x| ist , dann muss doch noch ein Fall 0<x<1 sein oder?
wenn ja wie geht es weiter?
Problem/Ansatz: