Tangentensteigung berechnen

Question

Aufgabe:

f(x)=3*x^2+x-2

An welcher Stelle besitzt die Funktion eine Tangente mit der Steigung 7?

Ansatz:

f'(x)=7

f'(x)=6*x+1

Muss ich die beiden Gleichungen vielleicht gleichsetzen?

LG

Answer 1

Muss ich die beiden Gleichungen vielleicht gleichsetzen?

f'(x)=6*x+1

Das ist ja deine Ableitung.

Diese setzt du nun 7, also ja.

\(f'(x)=6x+1=7 \Leftrightarrow x=1\)

Answer 2

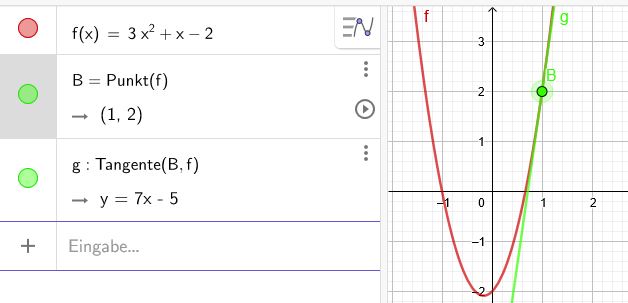
\(f(x)=3\cdot x^2+x-2\)

An welcher Stelle besitzt die Funktion eine Tangente mit der Steigung \(m=\red{7}\)?

Berechnung ohne Ableitung:

Ich schneide die Gerade \( y=\red{7}x+n\) mit der Parabel

\(3\cdot x^2+x-2=\red{7}x+n\)
\(3\cdot x^2-6x=2+n\)

\( x^2-2x=\frac{2+n}{3}\)

\( (x-\green{1})^2=1+\frac{2+n}{3}\)

\(x=\green{1}\) ist die Berührstelle.

Comments

Aus Deiner letzten Gleichung geht für x=1 hervor, dass n=-3 ist. Wie hast Du -5 in Deiner grafischen Darstellung erhalten?

---

3·x^2 - 6·x - 2 - n = 0

Diskriminante ist gleich Null

D = b^2 - 4·a·c = (-6)^2 - 4·3·(-2 - n) = 0 → n = -5

Wenn man eine Gleichung durch 3 teilt sollte man schon jeden Summanden durch 3 teilen, sonst wird das nix.

---

Danke für das Mehraugenprinzip!

---

Jetzt hast Du es verschlimmbessert, jetzt wäre n=-2…

---

Ist verbessert, Danke!