Hallo Hopeful,
Das LGS steht in der Aufgabenstellung:$$E_1: \space 6x_1-x_2+x_3=6 \\ E_2: \space 2x_1+x_2-x_3=-2$$ vielleicht siehst Du, dass durch eine Addition der Gleichungen bereits zwei der drei Variablen entfallen:$$E_1 + E_2: \implies 8x_1 = 4 \implies x_1 = \frac 12$$ Wähle ich \(x_3\) als freie Variable \(t\) und setze alles in \(E_1\) ein, so erhält man:$$\begin{aligned}x_3 &= t \\ 6 \cdot \frac 12 - x_2 + t &= 6 \implies x_2 =-3 + t\end{aligned}$$und jetzt nochmal alles sauber hinschreiben:$$\begin{aligned} x_1 &= \frac 12 && + & 0 \cdot t \\ x_2 &= -3 &&+ & 1 \cdot t \\ x_3 &= 0 &&+ & 1 \cdot t\end{aligned}$$und in Vektorschreibweise wird die Schnittgerade sichtbar:$$g: \space \vec{x} = \begin{pmatrix} \frac 12\\ -3 \\ 0 \end{pmatrix} + \begin{pmatrix} 0\\1 \\ 1\end{pmatrix}t$$
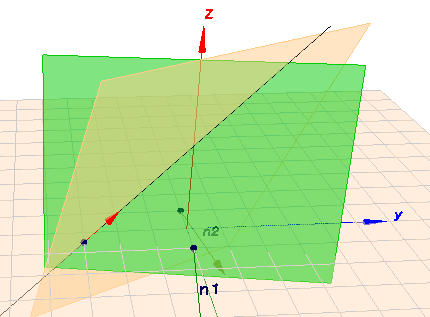
(klick auf das Bild und rotiere die Szene mit der Maus)
Oben siehst Du die Ebenen \(E_1\) (grün) und \(E_2\) (hellbraun) und die Gerade \(g\) von oben. So sieht man sofort, dass das Ergebnis sinnvoll ist.
Bei Aufgabe b) $$E_1: \space 4x_2=8 \\E_2: \space 2x_1+6x_3=0$$ folgt aus \(E_1\) unmittelbar \(x_2=4\). Ich setze wieder \(x_3=t\) und man erhält:$$g: \space \vec{x} = \begin{pmatrix} 0\\2 \\ 0 \end{pmatrix} + \begin{pmatrix} -3\\0 \\ 1 \end{pmatrix} t$$
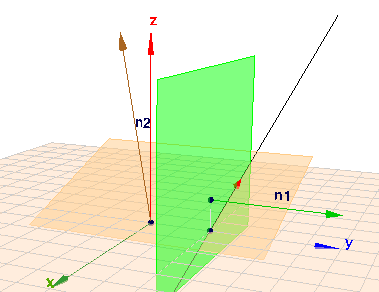
... und so sieht es in Geoknecht3D aus. (klicken und drehen)
Gruß Werner