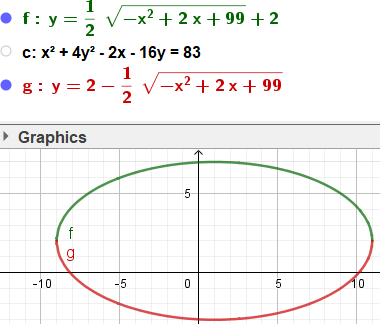
Nun, diese Quadrik ist eine Ellipse
2 (x-1)^2 +8 (y-2)^2 = 200
das kann man verschlimmbessern mit
(y - 2)² = (200 -2(x - 1)²)/8
|y - 2| = (1 / 2 * sqrt((-x^(2)) + (2 * x) + 99))
y = (1 / 2 * sqrt((-x^(2)) + (2 * x) + 99)) + 2
y = 2- (1 / 2 * sqrt((-x^(2)) + (2 * x) + 99))