Hier schon mal 3 mögliche Bildungsvorschriften:
http://www.gerdlamprecht.de/Roemisch_JAVA.htm#(x-2)*(x-4)*(7*x*x-43*x%20+%2046)*x/30@Ni=0;@N@Bi]=Fx(i);@Ci]=(i%252)*(i+1)/2;aD[i]=(@P-1,i+1)+1)*(i+1)/4;@Ni%3E9@N0@N0@N#
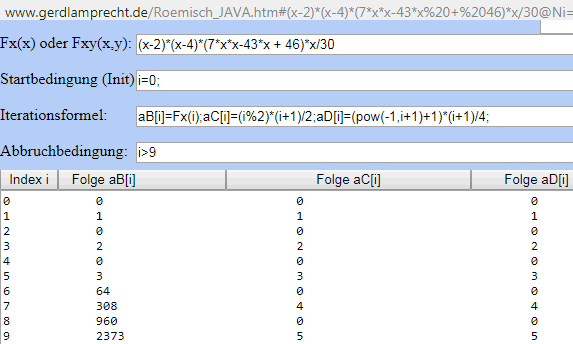
aB) (x-2)*(x-4)*(7*x*x-43*x + 46)*x/30 = (7 x^5)/30 - (17 x^4)/6 + 12 x^3 - (62 x^2)/3 + (184 x)/15
stimmt also Dein Polynom. Nur wegen der Rundungsfehler habe ich die Produktschreibweise dem Iterationsrechner übergeben.
Wenn man beim Polynom Grad 5 bleibt (man kann auch mit Grad 6 oder höher was basteln -> mathe ist grenzenlos),
lautet das nächste Glied aB[6]=64.
Ich glaube, dass nur von den Lehrern rübergebracht werden soll, dass Polynome zwar immer funktionieren, aber für viele physikalische Folgen ungeeignet sind.
aC und aD gehen von der viel einfacheren Folge aus, die bei geraden Gliedern 0 und bei ungeraden Gliedern ansteigend ist.
Dann gibt es noch Bruch-Algorithmen wie
1000/9801 = 0.102030405060708091011121314151617181920...
Es gibt auch ein Poynom, dass bei aB[6]=0 werden kann:
x*344/15-pow(x,2)*2026/45+pow(x,3)*32-pow(x,4)*187/18+pow(x,5)*47/30-pow(x,6)*4/45
Einfach bei http://www.gerdlamprecht.de/Mittelwerte.html
bei y[i]: 0, 1, 0, 2, 0, 3,0 eingeben und unten kopieren.
Die fertige Formel kann man zum Iterationsrechner kopieren -> fertig (nur mit Rundungsfehler, da intern mit double gerechnet wird)
Mit diesem Polynom Grad 6 ist dann aB[6]=0 und aB[7]=-140