Tangente mit der Steigung m=4 zu f(x) = -x2+2 finden

Question

Gegeben ist die Funktion f(x) = -x^2 + 2
An welcher Stelle x0 nimmt die Steigung der Tangente den Wert m=4 an?

Brauche Hilfe wie man sowas rechnet!

Answer 1

Nun, die Tangentensteigung an einer Stelle x₀ entspricht ja der Steigung des Funktionsgraphen an dieser Stelle. Diese aber berechnet man mit der ersten Ableitung von f ( x₀ ) .

Die zu lösende Gleichung ist also

f ' ( x₀ ) = 4

Die Ableitung von f ( x ) = - x ² + 2  ist: f ' ( x ) = - 2 x , also:

<=> - 2 x₀ = 4

<=> x₀ = 4 / - 2 = 2

An der Stelle x₀ = 2 nimmt also die Steigung der Tangenten an den Graphen von f ( x ) den Wert 4 an.  

Answer 2

Gegeben ist die Funktion $f(x) = -x^2 + 2$
An welcher Stelle x0 nimmt die Steigung der Tangente den Wert $m=4$ an?

Die Gerade $y=4x+8$ hat die Steigung $m=4$

$f(x)=y$

$-x^2 + 2=4x+8$

$-x^2 =4x+6$    

$-x^2-4x=6$   

$x^2+4x=-6$ 

$x^2+4x+4=-6+4$

$(x+\red{2})^2=-2$

Der Berührpunkt der Tangente ist nun $B(-\red{2}|-2)$

Comments

Die Gerade $y=4x+8$ hat die Steigung $m=4$

Das hat die Gerade $y=4x-41392087541937$ auch. Und die +8 fällt einfach so vom Himmel ?!

---

Es klappt auch mit der Geraden $y=4x+b$

---

Deine Antworten wirken dennoch immer so, dass alles vom Himmel fällt, was wohl daran liegt, dass du meistens alle Schritte unkommentiert lässt. Für Leute, die sowieso schon Probleme mit Mathe haben, sind solche Lösungen dann gar nicht mehr nachvollziehbar.

Da ist übrigens auch ein Rechenfehler in der Rechnung und die Tangente ist ja offensichtlich auch eine andere. Und dass die Gleichung $(x+2)^2=-4$ keine Lösung hat, ist offenbar auch egal.

---

Da ist übrigens auch ein Rechenfehler in der Rechnung und die Tangente ist ja offensichtlich auch eine andere.

Was ist an der Tangente falsch?

Und dass die Gleichung $(x+2)^2=-4$ keine Lösung hat, ist offenbar auch egal.

Ja, das ist egal, weil es hier nicht um eine Lösung der Gleichung geht, sondern nur um den Berührpunkt der Tangente. Der ist nun $B(-2|-2)$.

---

Deine Begründung ist Käse, weil sie falsch ist. Und das genau deswegen, weil deine Rechnung falsch ist. Deine Schlussfolgerung aufgrund einer falschen Rechnung, halte ich für kritisch. Du konstruierst hier also wieder irgendeinen Müll, anstatt einfach die Stelle zu berechnen, wo die Steigung genau der Steigung der Tangente entspricht. Aber das wurde ja in der anderen Antwort schon gemacht. Also fabriziert man lieber irgendeinen Mist, damit es inhaltlich etwas anderes ist.

Oben ist von der Geraden $y=4x+8$ die Rede. Als Tangente steht in dem Bild nun $y=4x+6$. Wie man nun also von der einen Geraden zur anderen kommt, findet sich hier nirgends wieder. Und warum diese Gleichung, die ja nicht gelöst werden muss, auf diese urkomische Weise den Berührpunkt liefert, ist ebenfalls für jeden Mathe-Laien nicht nachvollziehbar. So schön der Ansatz auch sein mag, die Ausführung ist schlicht eine Katastrophe und das hat mit Mathematik nicht mehr viel zu tun.

---

Wahrscheinlich hat er was gegen das Vorhaben, dass solche Aufgaben durch

(1) künstliche

(2) Intelligenz

beantwortet werden sollen.

Dann wählt man lieber bei mindestens einem der Parameter das Gegenteil.

---

Du Unbedarfte kann immer noch unterscheiden, wer ein freundlicher, wohlwollender und wer ein unfreundlich-aggressiver Helfer ist.

---

Man beachte meine ersten Kommentare und das Desinteresse von Moliets. Das hat nunmal mit Mathematik wenig zu tun und sollte hier gar nicht erst veröffentlicht werden, weil es alles andere als hilfreich ist. Gründe siehe oben. Solch eine Ignoranz von Helfern darf man ja wohl mit der entsprechenden Vehemenz begegnen. Wer hier also nicht wohlwollend ist, ist Moliets, weil er seine Nicht-Mathematik auf Biegen und Brechen versucht zu verteidigen.

---

Ich habe diesmal aufgepasst und mich nicht mit der Antwort auf über 10 Jahre alte Fragen (die auch vor über 10 Jahren schon beantwortet wurden) beschäftigt.

Erkennbar ist, dass es hier nicht um "helfen" geht, denn 1. liegt es dazu zu weit zurück und 2. werden kommentarlos Formeln/Terme aneinandergereiht, deren Zusammenhang mysteriös ist.

Es geht also, wie bei anderen "Helfern" auch, nur um den "Helfer" selbst.

---

Vielleicht ist das nun ein Beleg dafür, dass ich keinen "Mist" verzapft habe!

Es sei die Parabel $f(x)=3x^2-9x+6$ gegeben . Es sollen nun Tangenten an die Parabel parallel zu $y=m\cdot x-12$ gefunden werden.

$3x^2-9x+6=m\cdot x-12$

$3x^2-9x=m\cdot x-18$

$x^2-3x-\frac{m}{3}\cdot x=-6$

$x^2-x \cdot (3+\frac{m}{3})+(1,5-\frac{m}{6})^2=-6+(1,5-\frac{m}{6})^2$

$[x-(1,5+\frac{m}{6})]^2=-6+(1,5-\frac{m}{6})^2$

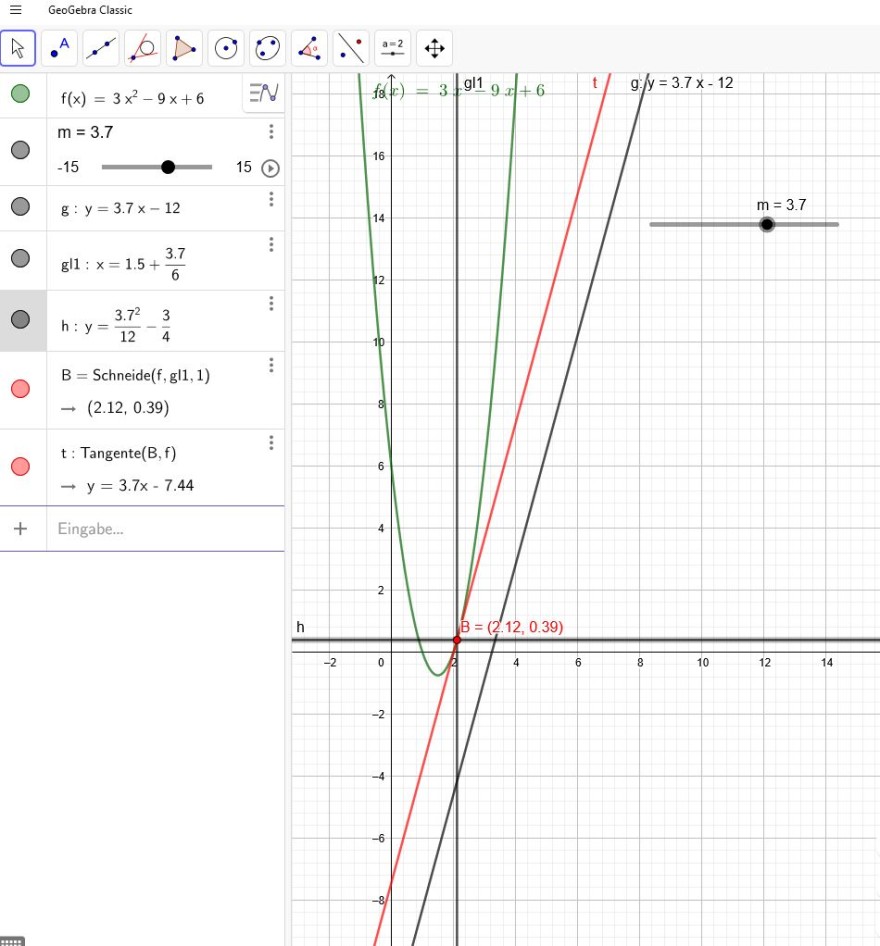
Der Berührpunkt hat nun die Koordinaten $B(1,5+\frac{m}{6}|\frac{m^2}{12}-\frac{3}{4})$

.

---

Dieses lückenhafte Stückwerk bestätigt in bester Weise den Vorwurf von Ampelmännchen.

Hätte ein real existierender Fragesteller diese Aufgabe gestellt, wäre er nach dieser "Antwort" noch verwirrter als vorher.

---

Hätte ein real existierender Fragesteller diese Aufgabe gestellt

Solche Art von Aufgaben sind mir auch noch nicht begegnet. Habe mir aber Gedanken gemacht, wie man das lösen kann. Es soll ein Beleg sein, dass man solche Aufgaben nicht nur herkömmlich lösen kann.

Wie würdest du meine Aufgabe denn lösen?

---

Wie würdest du meine Aufgabe denn lösen?

Man sucht natürlich zweckmäßigerweise nach den Stellen, wo die erste Ableitung den Wert m annimmt.

DU hast die Funktion mit JEDER Gerade der Schar gleichgesetzt, mit deinem Lieblingsspielzeug "quadratische Ergänzung" die x-Koordinate/n des Berührungspunktes/der Schnittpunkte gefunden (oder auch nicht, denn sie existieren nicht immer), um dann aus diesen unendlich vielen Möglichkeiten (oder Nicht-Möglichkeiten) völlig kommentarlos eine herauszupicken und zu sagen "Die ist es".

Das ist für einen Schüler das glatte Gegenteil von Hilfe.

---

Ortslinie der Berührpunkte:

Koordinaten von B:

 $x=1,5+\frac{m}{6}$         $y=\frac{m^2}{12}-\frac{3}{4}$

$m=6x-9$

 $y=\frac{(6x-9)^2}{12}-\frac{3}{4}$

Diese Ortslinie ist identisch mit der Parabel $f(x)=3x^2-9x+6$

Somit liegen alle Berührpunkte auf der Parabel.

---

Dass alle Berührpunkte für eine Tangente an den Graphen von $f$ auf $f$ liegen erfordert keine Rechnung, sondern ist vollkommen klar, weil ein Berührpunkt auf dem Graphen von $f$ liegen muss. Sonst wäre es kein Berührpunkt...

Das ist, als würde ich beweisen wollen, dass 0 auch tatsächlich gleich 0 ist.

---

Meine Bestimmung der Ortslinie war ein Kommentar zu Abakus:

um dann aus diesen unendlich vielen Möglichkeiten (oder Nicht-Möglichkeiten) völlig kommentarlos eine herauszupicken und zu sagen "Die ist es".

---

Lass es einfach                .

Answer 3

Gegeben ist die Funktion f(x) = 2 - x². An welcher Stelle x0 nimmt die Steigung der Tangente den Wert m = 4 an?

f(x) = 2 - x²
f'(x) = -2x = 4 → x = -2

An der Stelle x = -2 hat die Funktion und damit auch die Tangente an dieser Stelle die Steigung 4.

Plotlux öffnen

f₁(x) = 2-x²f₂(x) = 4·(x+2)-2Zoom: x(-8…8) y(-6…6)

Comments

Lösung ohne Ableitung

f(x) = 2 - x²
t(x) = 4x + b

Wenn t eine Tangente von f ist dann haben diese beiden eine Berührstelle gemeinsam.

2 - x² = 4x + b
x² + 4x + (b - 2) = 0
x = -2 ± ...

x = -2 ist also die Berührstelle. Dabei muss die Diskriminante den Wert 0 annehmen.

Diskriminante

D = 4 - (b - 2) = 0 --> b = 6

Das ist das, was ich auch oben mit der Ableitung heraus hatte.