Warum ist die Distanz von dem Punkt x zu der Gerade g proportional zu <x-p, normierte Normale von g>

Question

Aufgabe:

ich frage mich gerade warum

ist die Distanz von dem Punkt x zu der Gerade g proportional zu <x-p, normierte Normale von g>

Als Formel:

dist(x) ≈ <x-p, normierte Normale von g>

<> Skalarmultipl.
Problem/Ansatz:

Lässt sich das herleiten?

LG

Answer 1

Das gilt natürlich nur im Zweidimensionalen, sieht dann etwa

so aus :

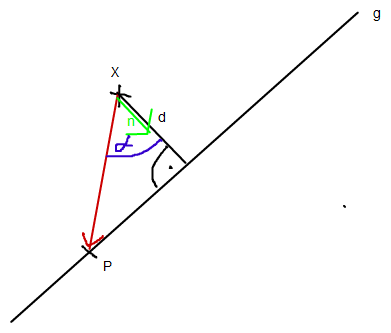
Hier gilt ja zum einen:   cos(α) =  d / |x-p|   #

(zumindest bei spitzem Winkel)

(denn |x-p| ist die Hypotenusenlänge (rot) )

Andererseits gilt ja für Vektoren immer

<x,y> = |x| * |y| * cos(α)

Und der Vektor von X bis zum Lotfußpunkt ist ja d*n

wenn n normiert ist .

Also hier   <Vektor XP, n > =  |x-p| * 1 * cos(α)

(Denn wenn n normiert ist, hat er ja Länge 1)

                     ==>      cos(α) =  <Vektor XP, n > / (  |x-p|)   ##

Gleichsetzen von # und ##

d / |x-p|     =   <Vektor XP, n > / ( |x-p|)

<=>  d = <Vektor XP, n >

Wenn also n der normierte Normalenvektor ist, dann ist

das schon der Abstand, und wenn n nicht normiert ist,

dann ist der Abstand zu dem Skalarprodukt halt nur proportional.

Comments

Vielen vielen Dank, sehr anschaulich erklärt! Oben fehlt noch ein # für die erste Gleichung, falls du es der Vollständigkeit halber hinschreiben möchtest. Schönes Wochenende