Flächeninhaltsverhältnisse von Dreiecken berechnen

Question

Aufgabe:

Gegeben seien die Dreiecke ∆ABC und ∆DEF, wobei die Seiten des Dreiecks ∆DEF dieselben Längen wie die Seitenhalbierenden des Dreiecks ∆ABC haben. Bestimmen Sie das Verhältnis S∆ABC:S∆DEF analytisch.

Problem/Ansatz:

Ich habe leider keine Idee und keinen wirklichen Ansatz für die Lösung dieser Aufgabe.

Die einzigen hilfreichen Formeln die ich dafür kenne sind die zur Berechnung der Seitenhalbierenden eines Dreiecks.

Answer 1

Die einzigen hilfreichen Formeln die ich dafür kenne sind die zur Berechnung der Seitenhalbierenden eines Dreiecks.

Na wunderbar.

Dann berechne die Längen der drei Seitenhalbierenden vom Dreieck ABC.

Kennst du auch eine Formel oder ein Verfahren, mit dem man den Flächeninhalt eines Dreiecks berechnet, von dem man alle drei Seitenlängen kennt?

Anderer Weg:

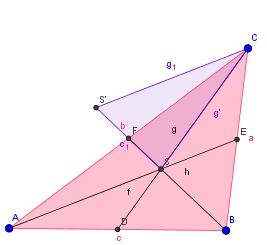
In der Abbildung ist SS' genau so lang wie BS.

1) Weise nach, dass die Seitenlängen des blauen Dreiecks jeweils zwei Drittel der Seitenhalbierenden des roten Dreiecks sind.

2) Begründe, dass das blaue Dreieck ein Drittel des Flächeninhalt des roten Dreiecks besitzt.

3) Mit welchem Faktor würde sich der Inhalt des blauen  Dreiecks erhöhen, wenn  man als Seitenlängen nicht zwei Drittel der Seitenhalbierenden verwendet, sondern die volle Länge der Seitenhalbierenden?

Comments

Also mit einem Beispiel mit irgendwelchen Zahlen bekomme ich das Verhältnis auch bestimmt, aber leider nicht allgemein.