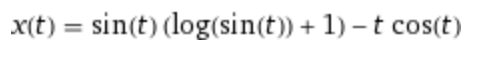Variation der Konstanten 1. Ordnung

Question

t^2*x' =x-1

wie muss ich diese Gleichung umformen damit ich sie mit Variation der Konstante lösen kann?

Ich habe Probleme mit der Umformung. Wie muss ich den Gleichungen immer umformen damit ich Variation der Konstante anwenden kann?

Gruß

Answer 1

warum Variation der Konstanten?. Diese DGL ist separierbar.

t^2 x'=x-1

t^2/dt =(x-1)/dx

dt/t^2=dx/(x-1)

-1/t +C = ln(x-1)

c*e^{-1/t}=x-1

c*e^{-1/t}+1=x

Answer 2

diese DGL kannst Du durch Trennung der Variablen lösen.

1. teile durch t^2

x'= (x-1)/t^2

dx/dt= (x-1)/t^2

dx/(x-1) =dt/t^2

usw

Comments

danke für eure Antworten aber ich habe andere Aufgaben die ich mit Variation der Konstante lösen muss...

Und weil ich die Umformung nicht verstanden habe bekomme ich immer Probleme..

Trennung der Variablen habe verstanden aber Variation der Konstante ist bisschen anders... Ich werde mich sehr freuen, wenn Sie mir das erklären können...

Erklären Sie mir bitte wie ich die Gleichungen für Variation der Konstante umformen muss...!

zb. x'sint-xcost = t     x(pi/2) =1

---

x' sin (t) -x cos (t)  = t    x(pi/2) =1

1 .)Du berechnest zuerst die homogene DGL:

x' sin(t) -x cos (t) = 0 (mittels Trennung der Variablen)

x_h= C₁ sin(t)

2.)  C₁= C(t)

x_p= C(t) sin(t)

Dann bildest Du  x_p'

_{3.) Dann setzt Du xp und xp' in die Aufgabe ein:}

_{(Der Term mit C(t) muß sich dabei kürzen)}

_{C(t)= ln|sin(t)| - t cot(t)}

_{4.) xp= C(t) *sin(t)}

_{5.)x =xh+xp}

_{6.) die AWB muß noch in die Lösung eingesetzt werden}

_Lösung:

---

ok verstanden.

ist das jetzt die explizite Durchführung der Variation der Konstante? Wenn ja gibt es auch eine allgemeine Lösungsformel?

Gruß

---

Es gibt diese 2 Möglichkeiten , ja auch die mit der Lösungsformel ist richtig .

Du muß es immer so machen, wie der Professor es macht, sonst gibt

es Punktabzug.

---

ist die Aufgabe bis dahin richtig?

---

unter Punkt 3 hast Du Dich verrechnet, es muß lauten:

C'(t) *sin^2(t)= t

---

Hallo so richtig?Upload failed: [object Object]

Wenn ich meine Anfangswerte einsetze bekomme ich bei C1=1

---

in der vorletzten und letzten Zeile fehlt ein t , sicher ein Schreibfehler , ansonsten ok

xp= sin(t) ln|sin(t)| - t cos(t)

x= .. analog fehlt hier das t für sin(t)

---

ja das war Tippfehlerr ......

Wenn ich die Aufgabe mit der allgemeinen Formel berechnen sollte, wie musste ich denn die Aufgabe berechnen?

Beste Grüße

---

Wie habt Ihr das denn auf der UNI gelernt?

---

Also das ist die Formel....