Warum funktioniert der Kosinussatz hier nicht?

Question

Zusammen

Wie rechne ich folgende Aufgabe richtig aus?

Aufgabe: Gegeben ist die abgebildete Raute (Rhombus) mit der Seitenlänge gleich der kürzeren Diagonalen . Drücken Sie
die Grösse der schraffierten Fläche in Abhängigkeit von s aus.

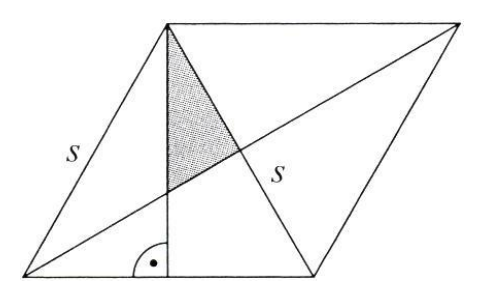
Mein Versuch:

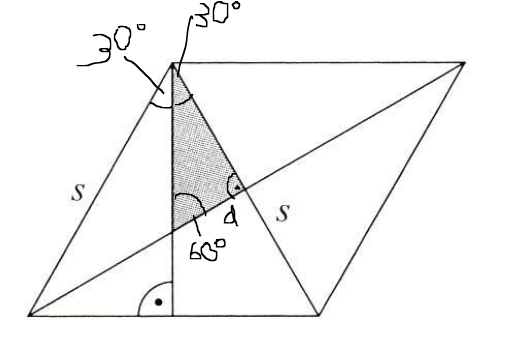
Das heisst ich habe zuerst d ausgerechnet und zwar so:

0.5s/sin(60) = d/sin(30) =d = s/(2*sqrt(3))

Ich glaube ich mache hier irgendwas falsch!

Dann die Fläche:

s/(2*sqrt(3)) * s = s²/(2*sqrt(3)) 

s²/(2*sqrt(3)) * 0.5 = (s²*sqrt(3))/12

Laut den Lösungen sollte ich auf (s²*sqrt(3))/24 kommen, was mache ich falsch?

Vielen Dank im Voraus!

LG
Toast

Answer 1

Zunächst die Höhe berechnen

(s/2)^2 + h^2 = s^2 --> h = √3/2·s

Jetzt direkt den Flächeninhalt berechnen

A = 1/2·(2/3·h)·(1/2·s)·SIN(30°)

A = 1/2·(2/3·(√3/2·s))·(1/2·s)·1/2

A = √3/24·s^2

Comments

Zu deiner Rechnung

d/SIN(30) = 0.5·s/SIN(60)

d = 0.5·SIN(30)·s/SIN(60) = 0.5·1/2·s/(√3/2) = √3/6·s

Jetzt noch die Fläche bestimmen

A = 1/2·(1/2·s)·d = 1/2·(1/2·s)·(√3/6·s) = √3/24·s^2

---

Danke vielmals, ich habe meinen Fehler so gefunden. Das Problem war, dass ich bei der Flächen Berechnung immer mit s gerechnet habe, statt mit 0.5s.

Vielen Dank!

LG
Toast