Aufgabe:
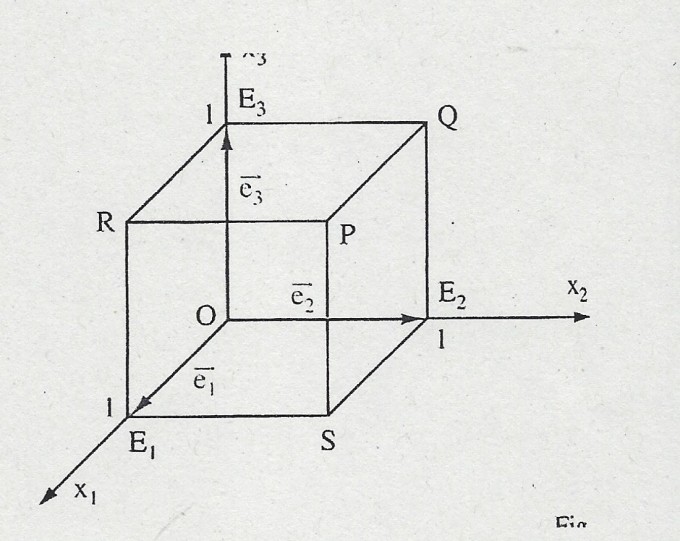
a) Begründen Sie: Die Vektoren e1, e2, e3 in Fig. 1 sind linear unabhänigig.
b) Stellen SIe jeden der Vektoren OP, E1Q, E2R, E3S als Linearkombination der Vektoren e1, e2, e3, dar.
c) Begründen Sie:
Jeweils drei der Vektoren OP, E1Q, E2R, E3S sind lineare UnAbhänig.
d) Stellen Sie jeden der Vektoren OP, E1Q, E2R, E3S als Linearekombination der derei anderen dar.
e1 , 2 ; OP... das sind alle Vektoren
Eigentliche Bezeichnungen:
E1Q = E1 Q
E2R = ....