Die Fläche unter einer Parabel durch Horizontale halbiert: f(x) = -3x^2 +3

Question

ich habe eine Hausaufgabe bekommen, komme jedoch nicht weiter. Eigentlich bin ich sehr gut in Mathe, bei dieser Aufgabe scheitern jedoch gute Freunde und mein Bruder mit frischem Abitur.

Zu sehen ist ein Koordinatensystem mit einer nach untengeöffneten Parabel die mit dem Faktor 3 getreckt wurde. Die ist um 3 Einheiten nach oben verschoben.

f(x) = -3x² +3

Die Aufgabe ist nun, eine horizontale Gerade zu finden, die den Flächeninhalt der o.g. Funktion halbiert. Ich habe schon in mehreren Foren nachgelesen, und kam dennoch nicht weiter. Lösungsansätze waren, die Funktion g(x) = a mit der Funktion f(x) gleichzusetzen und damit schonmal die Schnittpunkte zu finden. Weit gekommen bin ich damit jedoch auch nicht.

Vielleicht hat ja einer der hier aktiven schlauen Köpfe eine Idee? Ich wäre dir sehr dankbar.

Liebe Grüße, Lorenz
 

Answer 1

f(x) = -3·x^2 + 3
F(x) = 3·x - x^3

Fläche unter dem Graphen von f(x)

Nullstellen f(x) = 0
- 3·x^2 + 3 = 0
x = -1 ∨ x = 1

2 * ∫ (0 bis 1) f(x) dx = 2 * F(1) = 2 * 2 = 4

Gerade die die Fläche halbiert

g(x) = a

d(x) = -3·x^2 + 3 - a
D(x) = - x^3 - a·x + 3·x

Schnittpunkte von f ung g d(x) = 0

-3·x^2 + 3 - a = 0
x^2 = 1 - a/3
x = ±√(1 - a/3)

Fläche zwischen den Graphen f und g

2 * ∫ (0 bis √(1 - a/3)) d(x) dx = 2 * D(√(1 - a/3)) = 2 * (- √(1 - a/3)^3 - a·√(1 - a/3) + 3·√(1 - a/3)) = 2
-√(1 - a/3)^3 - a·√(1 - a/3) + 3·√(1 - a/3) = 1
a = 3 - (27/4)^{1/3} = 1.110118425

g(x) = 3 - (27/4)^{1/3}

Skizze:

Comments

Hallo Lorenz,
eine alternative Berechnung mit gleichem Ergebnis habe ich ebenfalls als Lösung eingestellt.
Der Mathecoach hat sie ebenfalls aufgegriffen und natürlich schneller als ich gelöst :-)

Auf seine Vorgehensweise wäre ich dagegen nie gekommen.
Er hat es halt drauf :-D


Besten Gruß

---

hallo coach! :-)

die aufgabe hatte ich auch gerade am wickel, aber, jetzt kann ich ja aufhören, weil du schneller warst. :-/

ich hatte erst h(x) = (1+x^3)/x und dann guckte ich doof aus der wäsche :D

pluspunkt!

---

Danke für eure Erklärungen!

Ich habe mir jetzt die ausführliche 1. vorgenommen und kann soweit folgen und finde es sinnvoll.
Wo ich jedoch nicht mehr mitkomme ist die auflösung nach a mit den Wurzeln!

Trotzdem vielen Dank!

---

Der geniale Brucy bringt mich da auf eine etwas verrückte Idee.

f(x) = √(x/3)
F(x) = √(4/27·x^3)

Nun soll die halbe Fläche von oben ja 1 sein.

F(x) = 1
√(4/27·x^3) = 1
4/27·x^3 = 1
x^3 = 27/4
x = (27/4)^{1/3}

Damit ist die horizontale Gerade bei 3 - (27/4)^{1/3}

Wir erhalten also die gleiche Lösung wie oben nur auf einem doch etwas geschickterem Weg.

:)

---

Wie kommst du auf F(x)?

---

Stammfunktion von 

f(x) = √(x/3) = (x/3)^{1/2}

Integrieren mit Kettenregel

F(x) = (x/3)^{3/2} / (3/2) / (1/3) = 2 * (x/3)^{3/2} = √(4/27·x³)

---

@ Mathecoach:
Danke für die Blumen :-D

Ich muss aber zugeben, dass ich auf Deine Lösung nie im Leben gekommen wäre!

Besten Gruß

---

Hey!
Kettenregel weiss ich eigentlich aber ich komme nicht auf F(x)... Wäre lieb wenn du das ganze einmal ausführlich herleitest!
viele grüße.

Answer 2

Hallo Lorenz, 

 

hier eine alternative Lösung:

Machen wir zunächst eine kleine Skizze des Sachverhalts. 

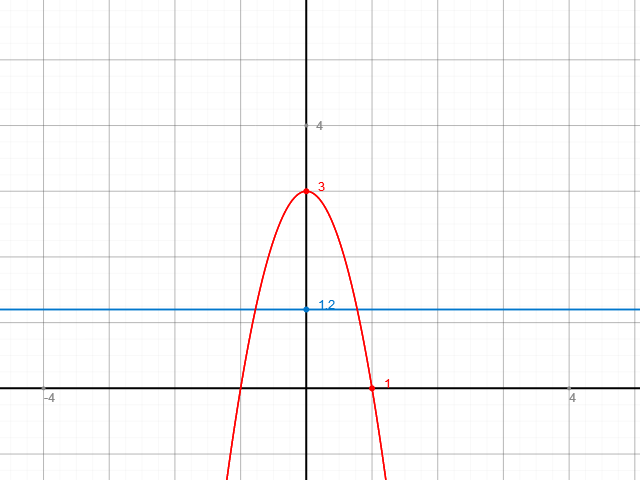
Wir betrachten nur die Seite links der y-Achse. Deren Flächeninhalt beträgt 2. Jetzt machen wir einen Trick und 

bestimmen die Umkehrfunktion, die etwa so aussieht: 

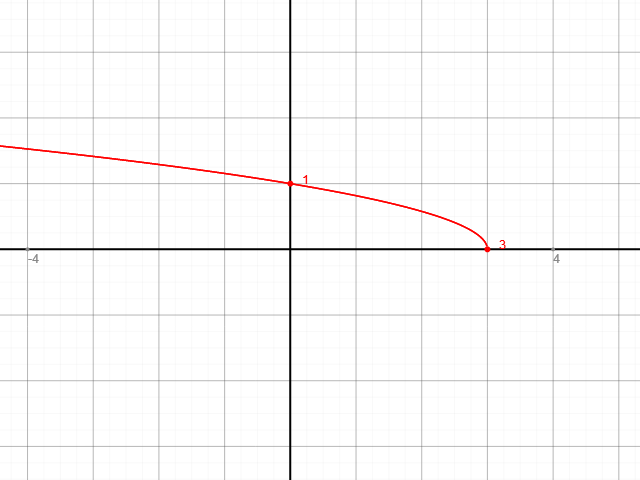
Herleitung der Umkehrfunktion: 

f(x) = -3x² + 3

x = -3y² + 3

x - 3 = -3y²

Die Umkehrfunktion lautet

g(x) = √[(x - 3)/(-3)] = (-x/3 +1)^1/2

G(x) = -2 * (1 - x/3)^3/2

Die Fläche unter dem Graphen von f(x) im Intervall von 0 bis 3 beträgt 2. 

Also suchen wir: 

G(x) - G(0) = 1

-2 * (1 - x/3)^3/2 + 2 * (1 - 0)^3/2 = 1 | :2

- (1- x/3)^3/2 + 1 = 1/2

(1 - x/3)^3/2 = 1/2 | hoch 2/3

x/3 = -(1/2)^2/3 + 1

x = 3 - 3*(1/2)^2/3 = 3 - 3*(1/4)^1/3 = 3 - (27/4)^1/3 

≈ 1,1101184252

Und diesen y-Wert schließlich hat die Gerade, die die Fläche unter f(x) halbiert.  

 

Besten Gruß